Задача 48130 ПОМОГИТЕ РЕШИТЬ ДАЮ 100 БАЛЛОВ...
Условие
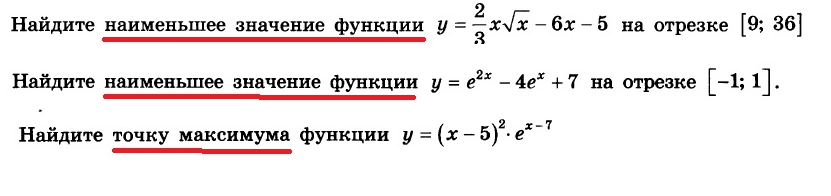
Решение
y`=((2/3)*x^(3/2) -6x-5)`=(2/3)*(3/2)*x^(1/2)-6=x^(1/2)-6=sqrt(x)-6
y`>0
sqrt(x)-6>0 ⇒ x >36
y` <0
sqrt(x)-6 <0 ⇒ 0 ≤ x <36
Функция убывает на [9;36]
Значит наибольшее значение в точке x=9, наименьшее в точке x=36
y(36)=(2/3)*36*sqrt(36)-6*36-5=4*36-6*36-5=36*(-2)-5=-72-5=-77
2.
f `(x)=e^(2х)*(2x)`-4e^(x)=2*e^(2x)-4*e^(x)
f ` (x)=0
2*e^(2x)-4*e^(x)=0
2*e^(x)*(e^(x)-2)=0
e^(x) > 0 при любом х
e^(x)-2=0
e^(x)=2 ⇒ x=ln2
-1 < ln (1/e) < ln2 < lne=1
в точке x=ln2 наименьшее значение
f(ln2)=e^(2ln2)-4e^(ln2)+7
Основное логарифмическое тождество:
e^(lnx)=x
x >0
f(ln2)=4-4*2+7=[b]3[/b] - наименьшее значение
3.
f`(x)=((x-5)^2)`*e^(x-7)+(x-5)^2*(e^(x-7))`=
=2*(x-5)e^(x-7)+(x-5)^2*e^(x-7)*(x-7)`=
=(x-5)*e^(x-7)*(2+x-5)=
=(x-5)*e^(x-7)*(x-3)
e^(x-7) > 0 при любом х
f`(x)=0
x-5=0 или x-3=0
x=5 или x=3
Знак производной:
___+__ (3) __-___ (5) __+__
х=3 - точка максимума
Все решения