Задача 34806 3)найти наименьшее и наибольшее значения...
Условие
y=e2x +1/ex, [–1;2]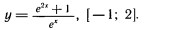

Все решения
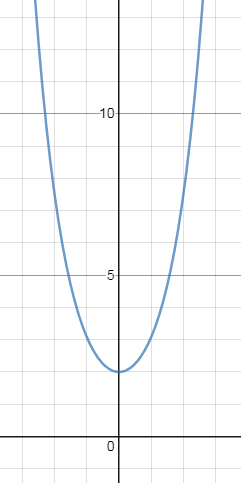
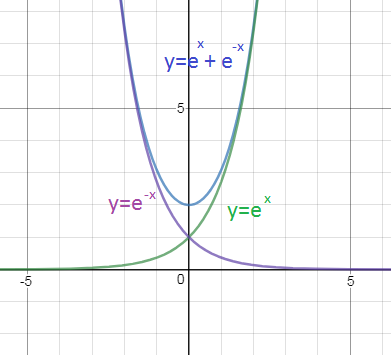
Перепишем функцию в виде :
y=e^(x)+ (1/e^(x))
или
y=e^(x)+e^(-x)
f(-x)=e^(-x)+e^(-(-x))
Функция является четной, так как
f(-x)=f(x)
y`=e^(x)+ e^(-x)*(-x)`
y`=e^(x)-e^(-x)
y`=0
e^(x)=e^(-x)
x=-x
x=0
Отмечаем знак производной на области определения
__-__ (0) __+__
x=0 - точка минимума
точка принадлежит отрезку [-1;2]
Значит при х=0 функция принимает наименьшее значение
значение на отрезке
y(0)=(1+1)/1=2
Находим значения на концах
y(-1)=e^(-1)+e
y(2)=e^(-2)+e^(2)
y(2)>y(1)
О т в е т. наименьшее значение в точке 0
y(0)=2
наибольшее значение в точке 2
y(2)=e^(-2)+e^(2)