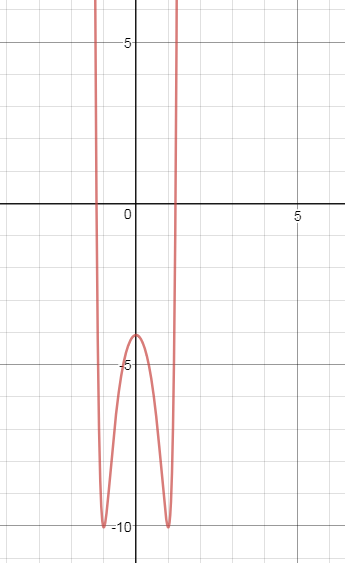
Задача 31909 ...

vk305555063

2018-12-13 23:29:48

y = e^(2x^2+1) × ( x^(2) - 3/2 ) исследовать на монотонность и экстремумы

Буду очень признателен, если будет решение до 7:00 по мск

Заранее Всем спасибо, за Ваш труд

sova

2018-12-13 23:49:26

★

y`=(e^(2x^2+1))`*(x^2-(3/2)) + e^(2x^2+1)*(x^2-(3/2))`=

=e^(2x^2+1)*(2x^2+1)`*(x^2-(3/2)) + e^(2x^2+1)*(2x)=

=e^(2x^2+1)*(4x*(x^2-(3/2))+2x)=

=e^(2x^2+1)*(4x^3-4x)

y`=0
e^(2x^2+1)> 0 при любом х

4x^3-4x=0

4х*(x^2-1)=0

x=0 или х= ± 1

Знак производной:

_-__ (-1) __+__ (0) __-__ (1) __+__

y`< 0 на (- ∞ ;-1) и на (0;1)
Функция убывает на (- ∞ ;-1) и на (0;1)

y`>0 на (-1;0) и на (1;+ ∞ )
Функция возрастает на (-1;0) и на (1;+ ∞ )

х=-1 и х=1 - точки минимума, производная меняет знак с - на +

y(-1)=y(1)=e^(3)*(-1/2)=-e^(3)/2

x=0 - точка максимума, производная меняет знак с + на -

y(0)=e*(-3/2)