Задача 62299 Найти уравнение касательной в точке...
Условие
Значения: x(t)=asin^3t,
y(t)=acos^3t,
t0=p/3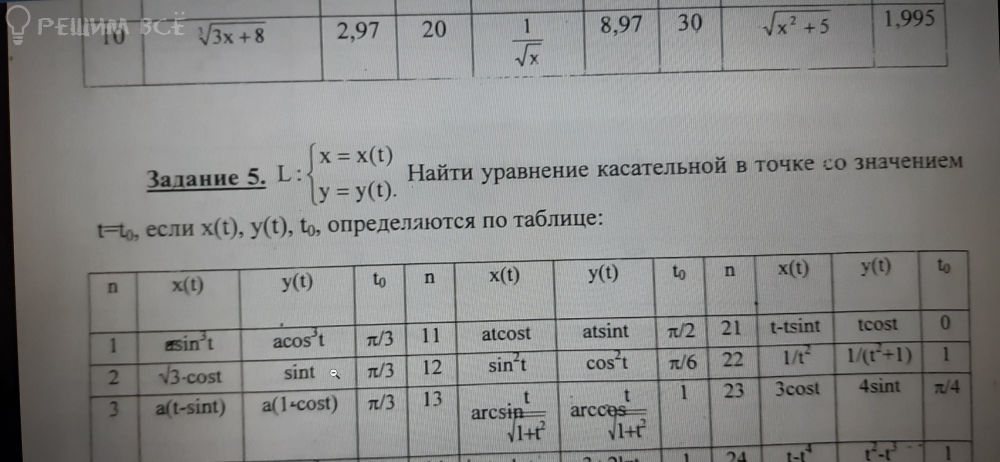
Решение
[m]x=a \cdot sin^3t[/m]
[m]y=a \cdot cos^3t[/m]
[m]y(\frac{π}{3})=a \cdot (cos\frac{π}{3})^3=a \cdot (\frac{1}{2})^3=\frac{a}{8}[/m]
[m]x(\frac{π}{3})=a\cdot (sin \frac{π}{3})^3=a \cdot (\frac{\sqrt{3}}{2})^3=\frac{3\sqrt{3}a}{8}[/m]
[m]y`_{x}=\frac{y`_{t}}{x`_{t}}[/m]
[m]y`_(t)=(a \cdot cos^3t)`=3 a \cdot cos^2t \cdot(cost)`=-3a \cdot cos^2t \cdot sint[/m]
[m]x`_(t)=(a \cdot sin^3t)`=3a \cdot sin^2t \cdot (sin t)`=3a \cdot sin^2t \cdot cost[/m]
[m]y`_(t_{o})=y`(\frac{π}{3})=-3a\cdot (cos\frac{π}{3})^2\cdot (sin\frac{π}{3})=-\frac{3a\sqrt{3}}{8}[/m]
[m]x`_(t_{o})=3a\cdot (sin \frac{π}{3})^2\cdot ( cos \frac{π}{3})=\frac{3a\sqrt{3}}{8}[/m]
[m]y`_{x_{o}}=\frac{y`_{t_{o}}}{x`_{t_{o}}}=-1[/m]
Подставляем в уравнение:
y-y_(o)=y`_(x_(o))*(x-x_(o))
[m]y-\frac{a}{8})=-1(x-\frac{3a\sqrt{3}}{8})[/m]
[m]y=-x+\frac{a\sqrt{3}}{4}[/m]
О т в е т. [b][m]y=-x+\frac{a\sqrt{3}}{4}[/m][/b]