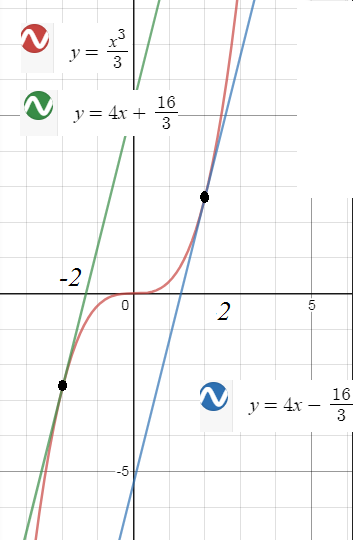
Задача 46557 К графику функции y=x^3/3 провести...

К графику функции y=x³/3 провести касательную так, чтобы она была параллельна прямой y=4x−4.

Уравнения касательных:

Параллельные прямые имеют одинаковые угловые коэффициенты

y=4x–4 – уравнение прямой с угловым коэффициентом k=4

Значит,

k_{касательной}=4

Геометрический смысл производной функции в точке:

f `(x_o)=k_{касательной}

Задача сводится к нахождению точек x_o, в которых производная равна 4

f `=(x<sup>3</sup>/3)`

f `=(1/3)·3x²

f `=x²

f`(x_o)=x_o²


x_o²=4

x_o=–2 или x_o=2

Теперь надо составить два уравнения касательной

в точке x_o=–2 и в точке x_o=2

в точке x_o=–2

f(–2)=(–2)³/3=–8/3

y–(–8/3)=4·(x–(–2))

y+(8/3)=4x+8

y=4x+(16/3)



в точке x_o=2

f(2)=(2)³/3=8/3

y–(8/3)=4·(x–2)

y=4x– (16/3)