Задача 45314 ...

vk188345384

2020-03-25 11:42:35

41.44. Определите абсциссы точек, в которых касательная к графику функции y = h(x) образует с положительным направлением оси абсцисс заданный угол α:
a) f(x) = x² - 3x + 19, α = 45°;
б) f(x) = 4/(x + 2), α = 135°.

sova

2020-03-25 12:06:55

f `(x_(o))=tg α
α - это угол, который образует касательная с положительным направлением оси Ох

a) α =45 ° ⇒ tg α = tg 45 ° =1

f `(x_(o))=1

f ` (x)=2x-3

f `(x_(o))=2x_(o)-3

2x_(o)-3=1

2x_(o)=4

[b]x_(o)=2[/b]

б)
α =135 ° ⇒ tg α = tg 135 ° = - 1

f `(x_(o))=- 1

f ` (x)=(4/(х+2))`

f ` (x)=-4/(х+2)^2


f `(x_(o))=-4/(х_(o)+2)^2

-4/(х_(o)+2)^2=-1

(х_(o)+2)^2=4

x_(o)+2=-2 или x_(o)+2=2

[b]x_(o)=-4[/b] или [b]x_(o)=0[/b]

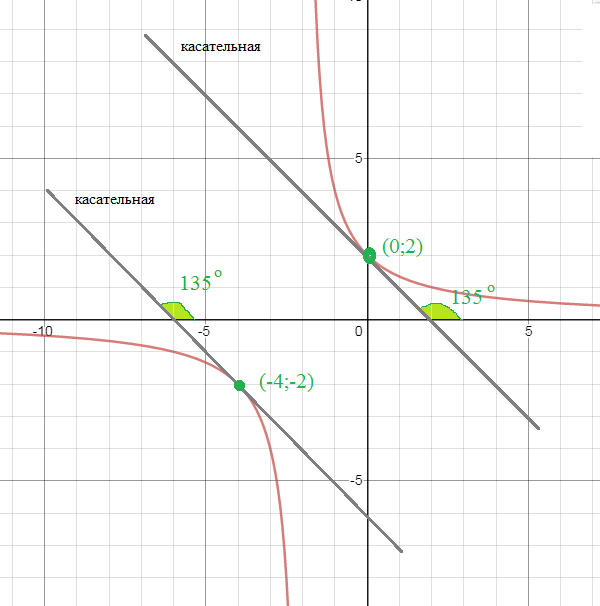
cм. рис.
Две касательные к гиперболе в точках
[b]x_(o)=-4[/b] и [b]x_(o)=0[/b]
образуют тупой угол в 135 ° с осью Ох