Задача 70353 Варіатн 1 ...
Условие

Решение
a)
Находим
f `(x)=(x^4)`=4x^3
[b]x_(o)=2[/b]
f(x_(o))=2^4=[red]16[/red]
f `(x_(o))=4*2^3=32
f `(x_(o))=[blue]32[/blue]
y=[red]16[/red]+([blue]32[/blue])*(x-[b]2[/b])
[b]y=32х-48[/b]- уравнение касательной
б)Находим
f `(x)=(x^2+4x)`=2x+4
[b]x_(o)=-1[/b]
f(x_(o))=(-1)^2+4*(-1)=[red]-3[/red]
f `(x_(o))=2*(-1)+4=2
f `(x_(o))=[blue]2[/blue]
y=[red]-3[/red]+([blue]2[/blue])*(x-[b](-1)[/b])
[b]y=2х-1[/b]- уравнение касательной
в)
Находим
f `(x)=(3*sinx-2)`=3*cosx
[b]x_(o)=-π[/b]
f(x_(o))=3*sin(-π)-2=[red]-2[/red]
f `(x_(o))=3*cos(-π)=3*(-1)=3
f `(x_(o))=[blue]3[/blue]
y=[red]-2[/red]+([blue]3[/blue])*(x-[b](-π)[/b])
[b]y=3х+3π-2[/b]- уравнение касательной
2)
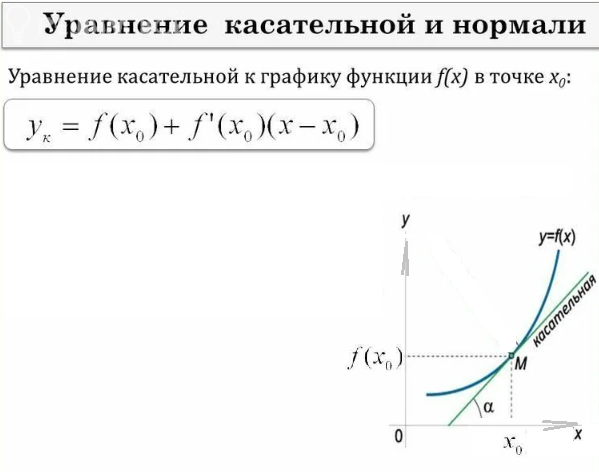
[b]Геометрический смысл производной в точке[/b]
у=kх+b - уравнение прямой [i]с угловым коэффициентом
[/i]
k_(прямой)=tg α
α -угол наклона прямой к [i] положительному направлению[/i] оси Ох
Касательная - это тоже прямая.
Геометрический смысл производной функции в точке :
[b]f`(x_(o)) =k_(касательной)[/b]⇒
Тангенс наклона касательной к графику функции y=f(x) в точке с абсциссой x_(o):
[red][b]tg α =f`(x_(o)) [/b][/red]
tg135=-1
Находим
f`(x)=[m](\sqrt{5-2x})`=\frac{1}{2\sqrt{5-2x}}\cdot (5-2x)`[/m]
f`(x)=[m]-\frac{1}{\sqrt{5-2x}}[/m]
f`(x_(o))=[m]-\frac{1}{\sqrt{5-2x_{o}}}[/m]
Приравниваем и получаем уравнение
[m]-\frac{1}{\sqrt{5-2x_{o}}}=-1[/m] ⇒ [m]\sqrt{5-2x_{o}}=1[/m] ⇒ [m]5-2x_{o}=1[/m] ⇒ [m]x_{o}=2[/m]
y_(o)=[m]\sqrt{5-2\cdot 2}=1[/m]
О т в е т. в точке [b](2;1)[/b]
3)
Касательная параллельна оси Ох
Значит k=0
[red][b]k =f`(x_(o)) [/b][/red] ⇒ [b]f`(x_(o))=0 [/b][
Находим производную:
[m]y`=(2x^3+3x^2+8x+1)`=6x^2+6x+8[/m]
Приравниваем:
[m]6x^2+6x+8=0[/m]
D=6^2-4*6*8<0
Уравнение не имеет корней.
Нет таких точек, о которых говорится в требовании задачи