Комплексные числа
О категории
Тригонометрическая, показательная форма комплексного числа. Действия над комплексными числами, возведение в степень, извлечение корня.Формула Муавра.
Практика (57)
Задание 10: пример на фото
Задание 11: пример на фото
Задание 46: пример на фото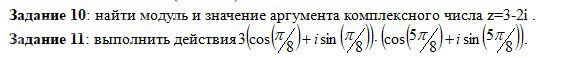
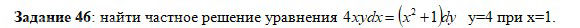
(1+i)¹⁰⁰⁰
|z| + z = 8 + 4i
(1+i)ⁿ
z² - (1+i).z +6+3i= 0
z^3 = -1 - i;
Z = (1-i)^7 / (1+1)^(13)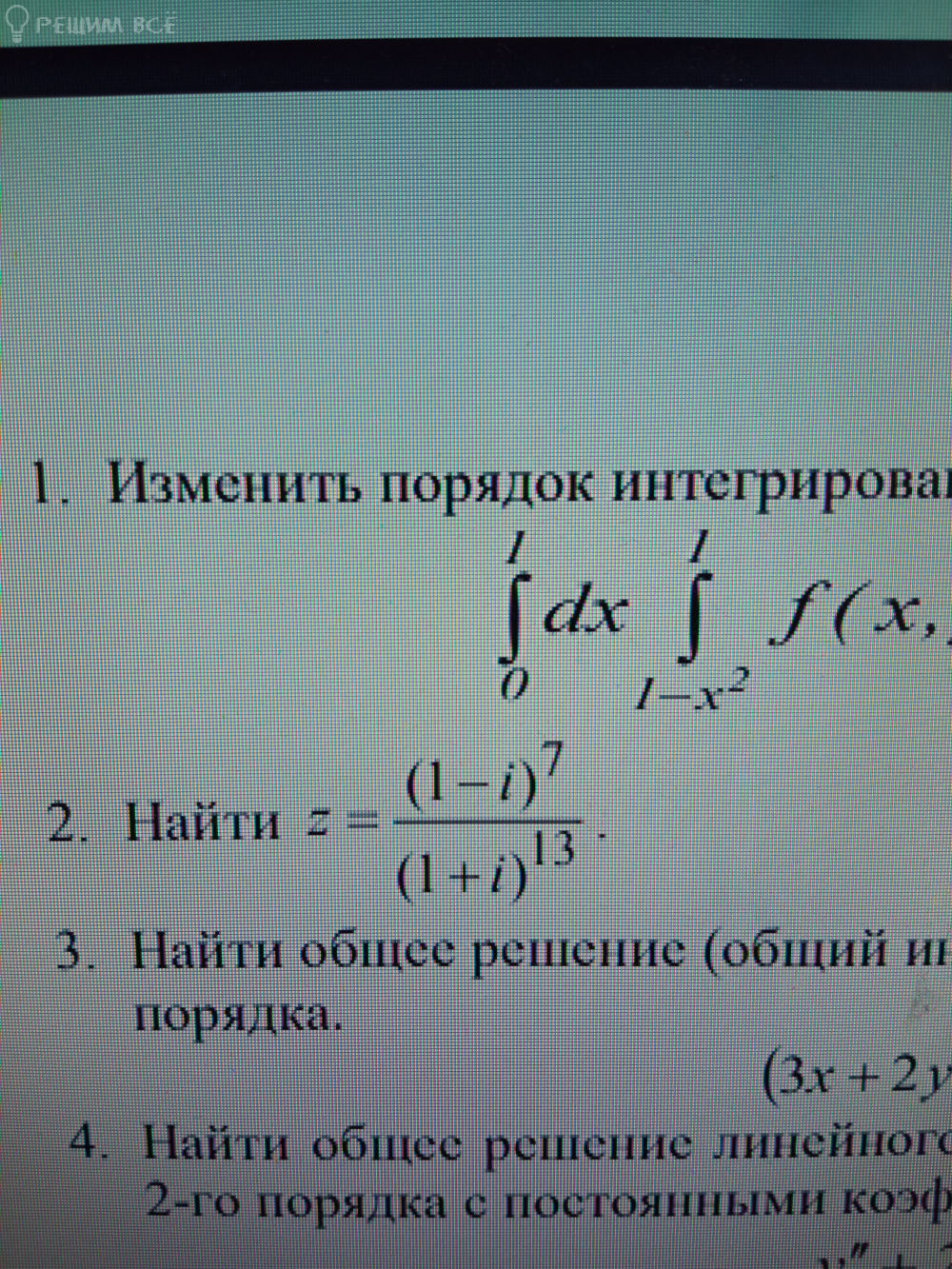
Z = (sqrt(3)/3 + sqrt(3)/3 I)^(100) 

Дано комплексное число a. Требуется: 1) записать число a в алгебраической и тригонометрической форме; 2)найти все корни уравнения z^3=a^2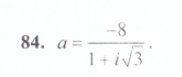


комплексными числами:
б) Решить уравнение. Корни
уравнения записать в
тригонометрической и
показательной формах. 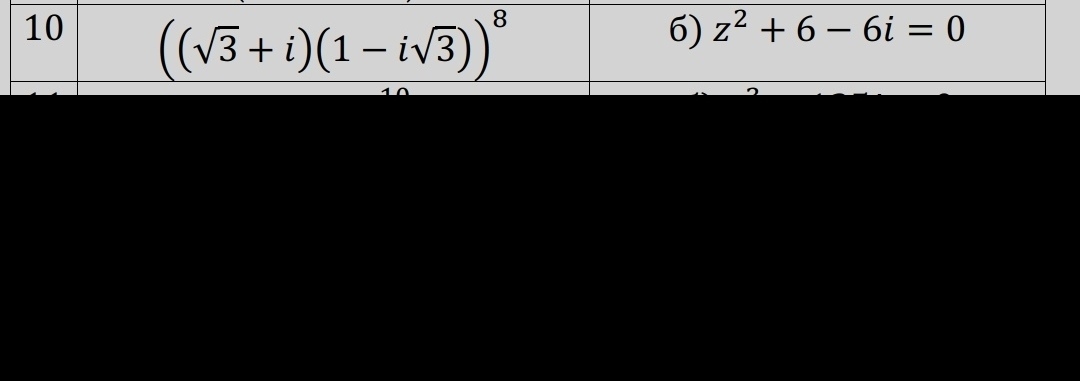

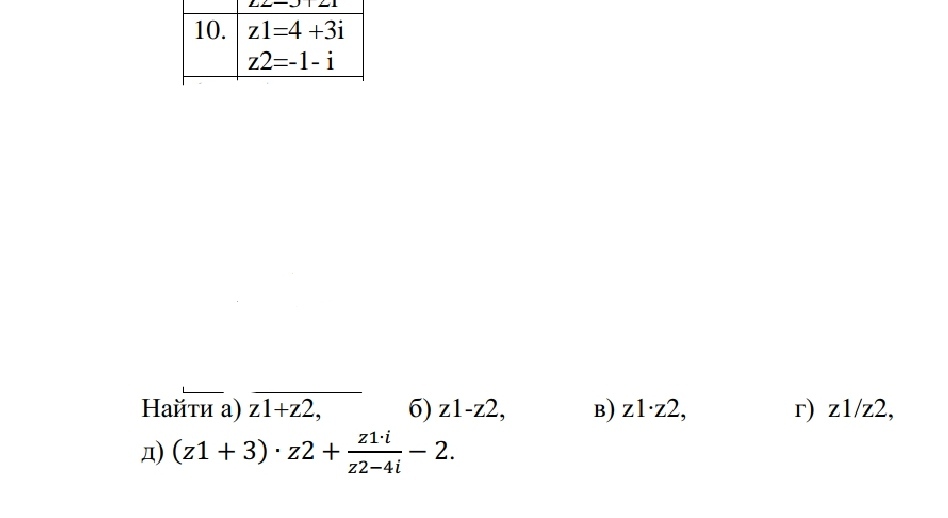
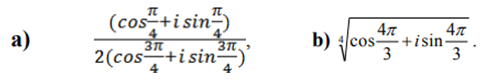
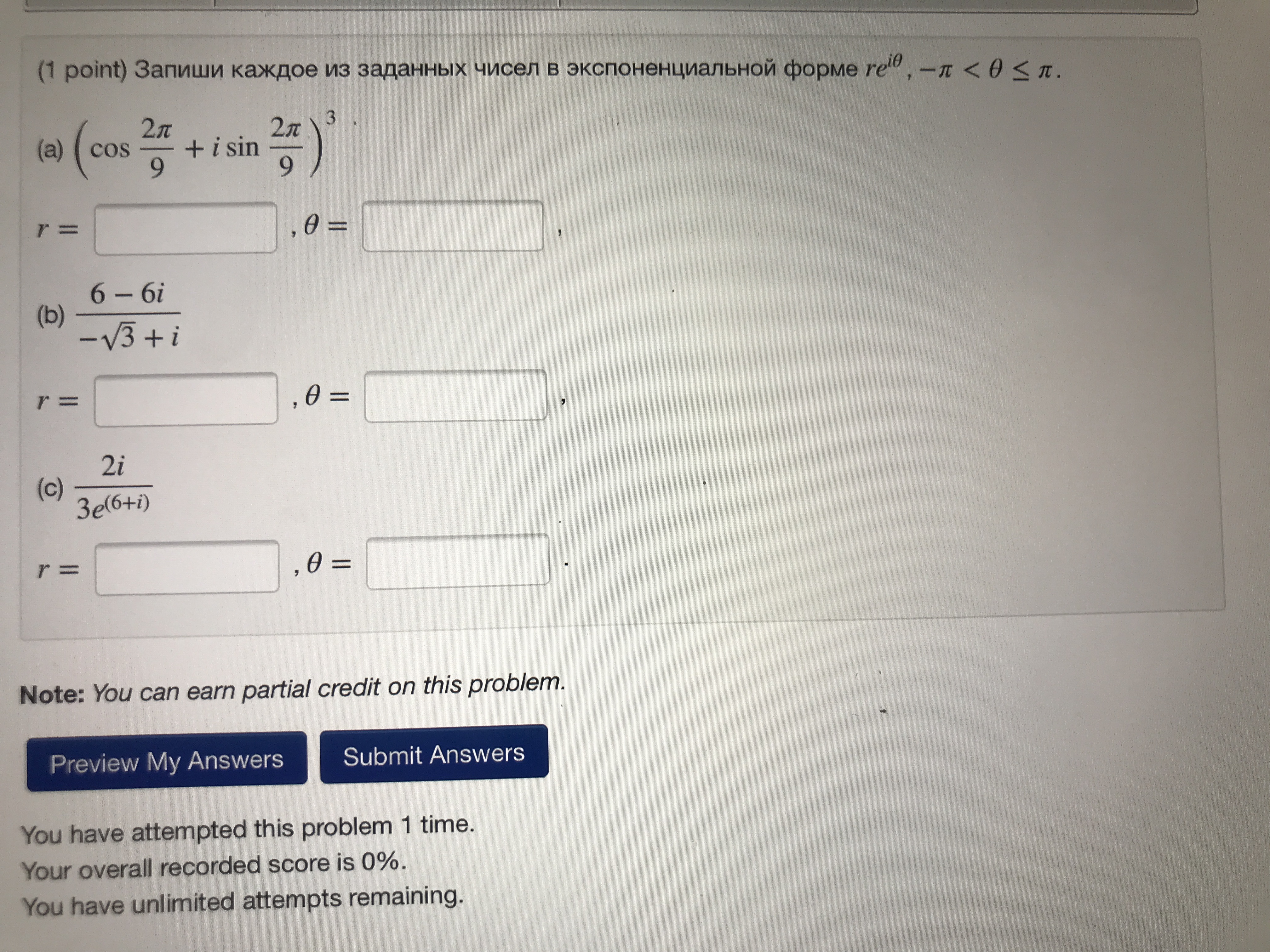
алгебраической, тригонометрической и показательной формах; 2)
изобразить его на координатной плоскости.
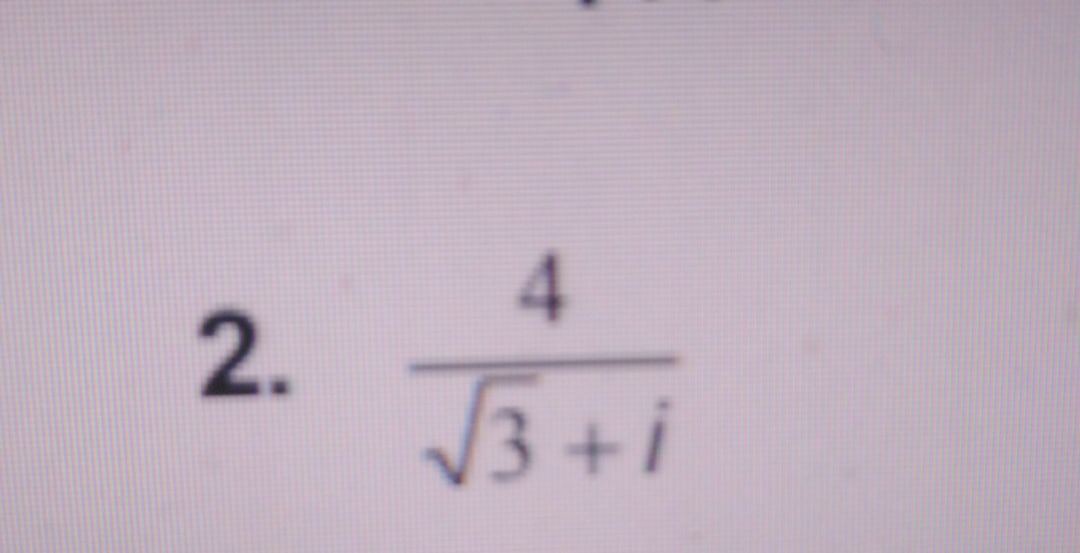
Помогите пожалуйста! Перевести в алгебраическую форму и решить (1+i)^8(1-√3i)^6
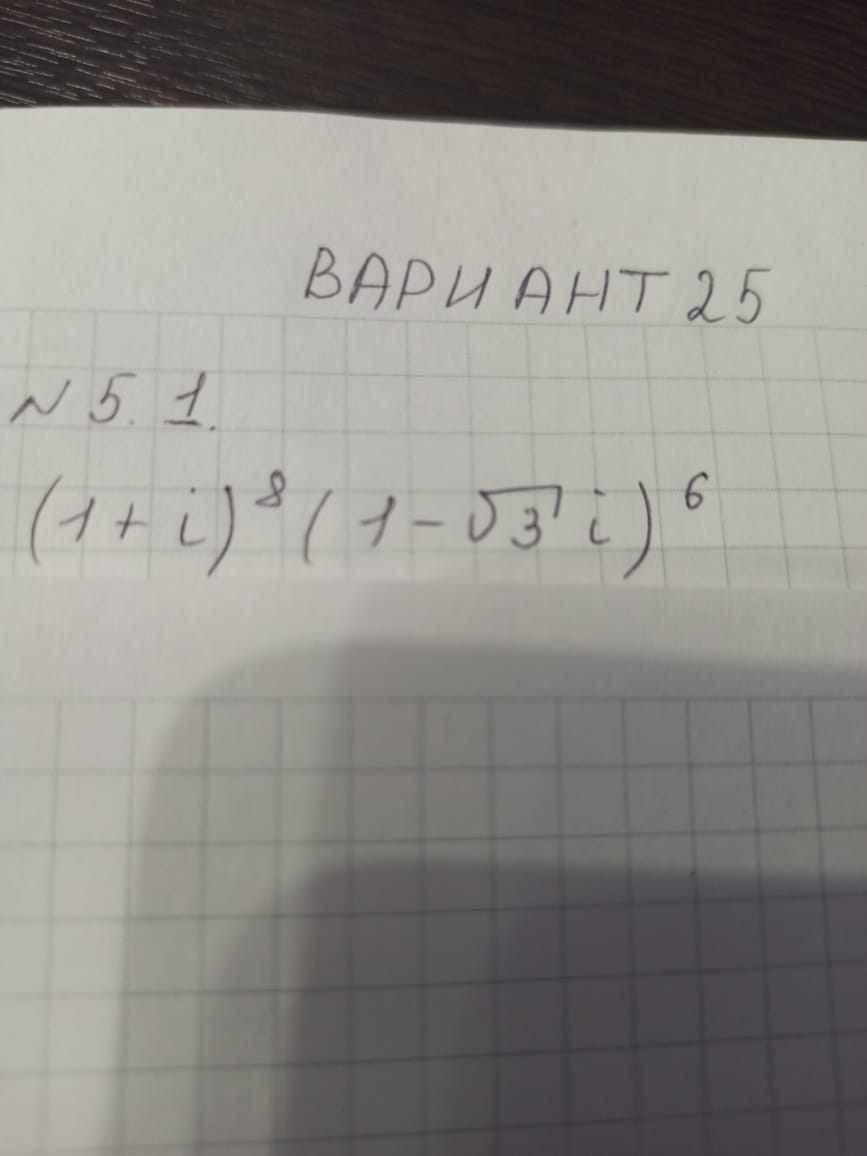
Задание 2. Представить комплексное число в тригонометрической и показательной формах.

Решить квадратное уравнение с действительными коэффициентами: x^2 + 2x + 5 = 0
r = 19,
φ = π/23
9) Вычислите z₁ : z₂ , используя показетельную форму записи комплексного числа, если z₁ = 14 ∙ e^(5π / 27 i), z₂ = 19 ∙ e^(- 4π / 9 i)


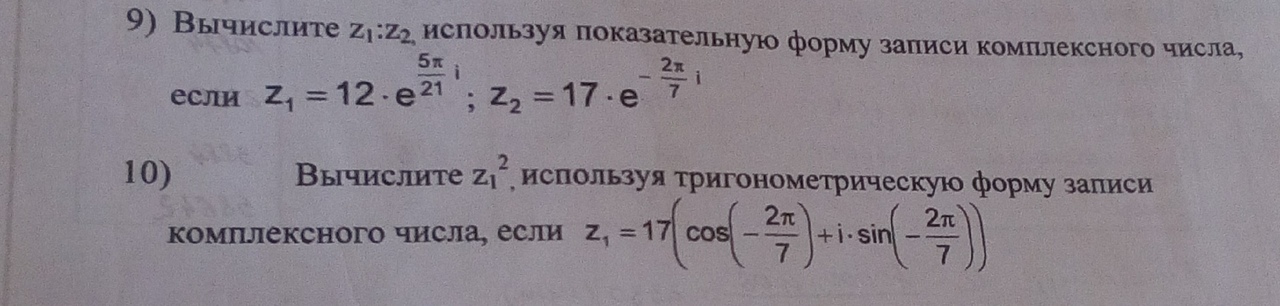

z=-4+4i
В ответ введите y.
Пример ввода ответа: 7

1) (3x²y - y³) / (x² + y²)
2) (x²y + xy²) / (x² + y²)
3) (-3xy - y³) / (x² + y²)
В ответ введите номер выражения.
Ответ округлите до трёх цифр после десятичной точки.
z=-4+4i перевести из алгебраической формы в тригонометрическую
z^2=a^2. помогите пожалуйста подробно решить
5. z1 = -2 + 2√3i ; z2 = 1 - i
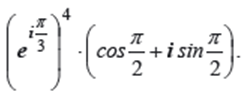

Z²+(3i-2)z+5-3i=0
z₁ = 4 + 3i, z₂ = 1 - √3i
Найти: ..
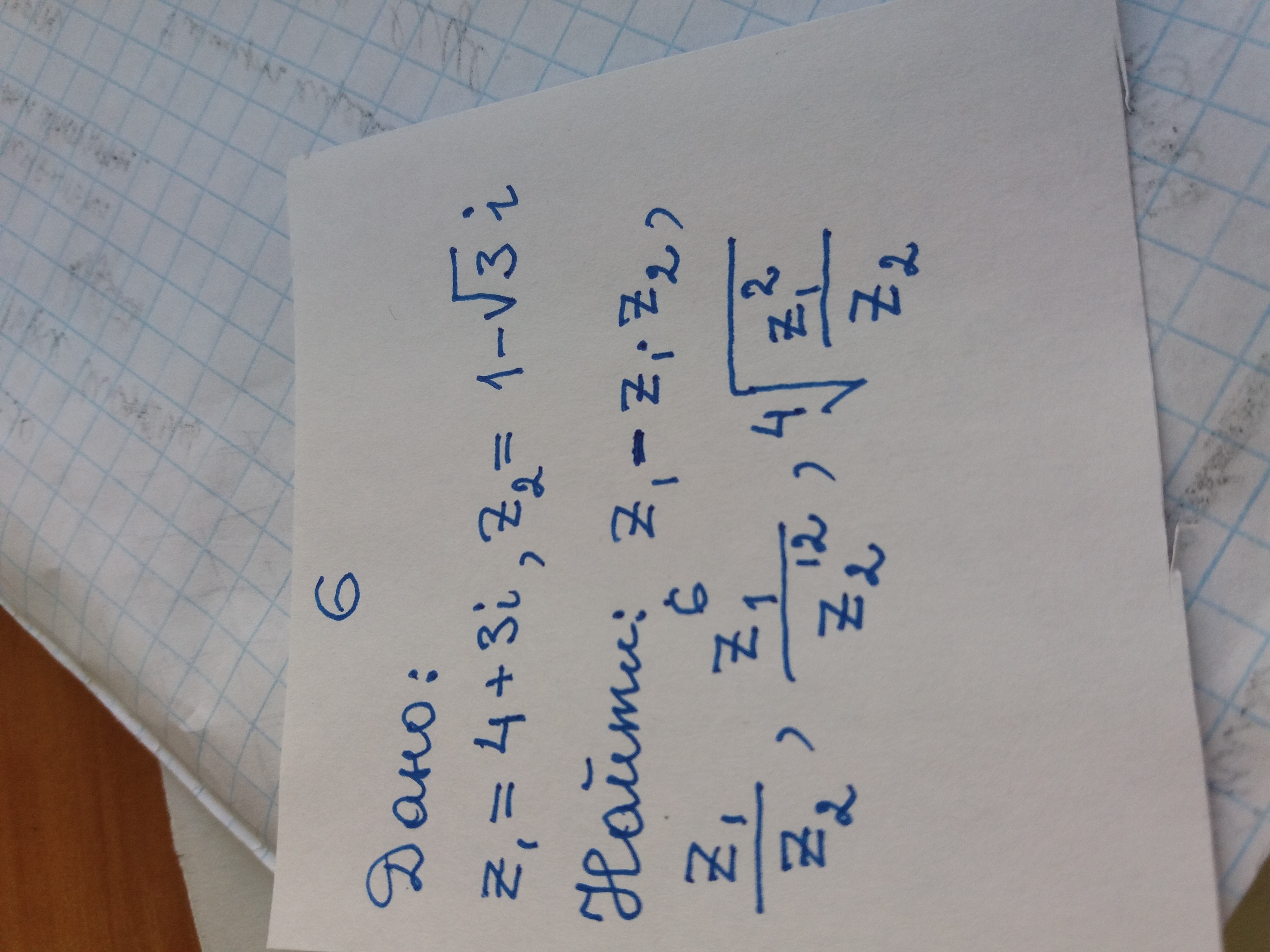

4. z1 = -1 - i; z2 = 2 + 2√3i

Даны комплексные числа z₁ и z₂ в алгебраической форме. Требуется найти: 1) z₁ + z₂ ; 2) z₁ - z₂ ; 3) z₁ * z₂ ; 4) z₁ / z₂ ; 4) z₁² - z̅₂.
4. z₁ = -1 - i ; z₂ = 2 + 2√3i
число a в алгебраической и тригонометрической формах; 2) найти все корни
уравнения z^3 + a= 0
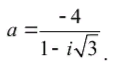
Редакторы (1)
 SOVA
SOVA
Создатель