Задача 34910 Дано комплексное число z . Требуется: 1)...
Условие
число a в алгебраической и тригонометрической формах; 2) найти все корни
уравнения z^3 + a= 0
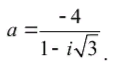
математика 10-11 класс
3850
Решение
★
a=x+iy
x=-1
y=-sqrt(3)
r=sqrt(x^2+y^2)=sqrt(4)=2
cos φ =x/r=-1/2
sin φ =y/r=-sqrt(3)/2
φ =-2π/3
a=r*(cos φ +isin φ )=2*(cos(-2π/3)+isin(-2π/3))=2cos(2π/3)-isin(2π/3)
a=r*e^(iφ )=2*e^(i*(-2π/3)+2πk), k ∈ Z
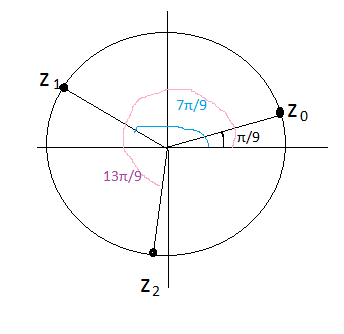
2.
z^3=1+sqrt(3)
1+sqrt(3)=2*(cos(π/3)+isin(π/3))
z^(1/3)=∛2* [b]([/b] cos(((π/3)+2πk)/3)+isin(((π/3)+2πk)/3) [b] )[/b]
при k=0
z_(0) [b]=∛2*(cos(π/9)+isin(π/9)[/b]
z_(1)=∛2*(cos(((π/3)+2π)/3)+isin(((π/3)+2π)/3)=
[b]=∛2*(cos(7π/9)+isin(7π/9))[/b]
z_(2) [b]=∛2*(cos(13π/9)+isin(13π/9))[/b]