Задача 61771 Комплексные числа, никак не могу...
Условие
Дано комплексное число a. Требуется: 1) записать число a в алгебраической и тригонометрической форме; 2)найти все корни уравнения z^3=a^2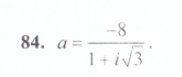

Решение
на (1-i·√3)
В знаменателе формула разности квадратов:
(1–i·√3)(1+i·√3)=1–(i·√3)2=1–i2·3=1+3=4
получим
a=–8·(1-i·√3)/4=-2·(1-i√3)=-2+2i√3 – это алгебраическая форма
a=x+iy
x=-2
y=2√3
|a|=√(x^2+y^2)=√((-2)^2+(2√3)^2)=4
cos φ =x/|a|=-2/4=-1/2
sin φ =y/|a|=2√3/4=√3/2 угол во второй четверти
⇒ φ =2π/3
a=4·(cos(2π/3)+isin(2π/3)) – тригонометрическая форма
========
a^2=(-2+2i√3)2=4-8i√3–12=–8-8·i√3
Теперь для этого числа надо найти тригонометрическую форму
|a^2|=√((–8)^2+(-8·√3)^2)=16
cos φ =–8/16=-1/2
sin φ =-√3/2 ⇒ угол в третьей четверти
φ =-2π/3
a:2=16·(cos(-2π/3)+i·sin(-2π/3))
Применяем формулу Муавра.
∛(–8-8·i√3)=∛16·[m](cos\frac{(-\frac{2π}{3})+2πk}{3}+isin\frac{(-\frac{2π}{3})+2πk}{3}), k ∈[/m] Z
при k=0
первый корень
z_(o)=∛16·[m](cos\frac{(-\frac{2π}{3})}{3}+isin\frac{(-\frac{2π}{3})}{3})=[/m]∛16·[m](cos\frac{(-2π)}{9}+isin\frac{(-2π)}{9})[/m]
при k=1
второй корень
z_(1)=∛16·[m](cos\frac{(-\frac{2π}{3})+2π}{3}+isin\frac{(-\frac{2π}{3})+2π}{3})[/m]=[/m]∛16·[m](cos\frac{(4π)}{9}+isin\frac{(4π)}{9})[/m]
при k=2
третий корень
z_(2)=∛16[m](cos[m]\frac{(-\frac{2π}{3})+4π}{3}+isin\frac{(-\frac{2π}{3})+4π}{3})[/m]=∛16·[m](cos\frac{(10π)}{9}+isin\frac{(10π)}{9})[/m]
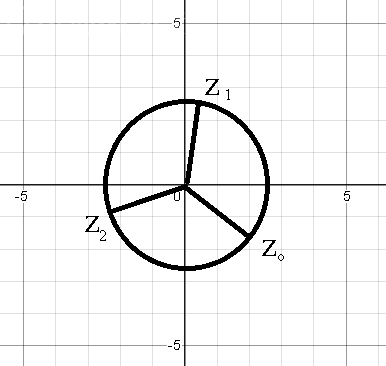
Корни расположены на окружности радиуса ∛16
Первая точка zo на пересечении окружности радиуса ∛16 и радиуса, образующего угол (-2π/9) c осью Ох
Вторая точка z1 на пересечении окружности радиуса ∛16 и радиуса, образующего угол (4π/9) c осью Ох
Вторая точка z2 на пересечении окружности радиуса ∛16 и радиуса, образующего угол (10π/9 )c осью Ох
Точки zo;z1;z2 делят окружность на [b]три[/b] ( потому что корень третьей степени) равные части, каждая по 120 °