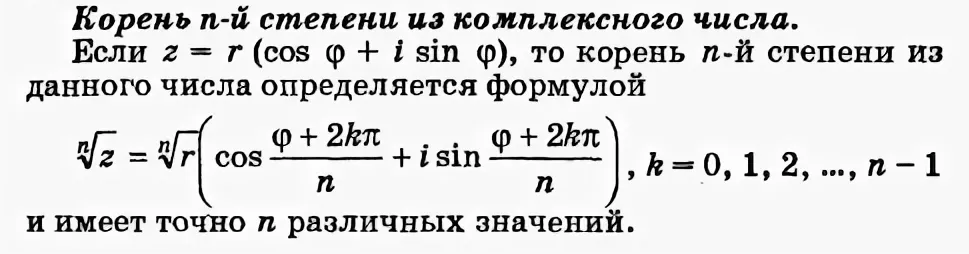Задача 42373 Дано комплексное число a=4/1-i ....
Условие
Решение
a=4*(1+i)/(1-i)*(1+i)=(4+4i)/(1-i^2)=(4+4i)/(1-i^2)=(4+4i)/2=2+2i - в алгебраической форме вида x+iy
при этом
x=2; y=2
см. переход от алгебраической к тригонометрической в приложении 1
|z|=sqrt(2^2+2^2)=sqrt(8)
tg φ =y/x=2/2=1 ⇒ φ =π/4
[b]a=sqrt(8)*(cos(π/4)+isin(π/4))[/b] - в тригонометрической форме
2)
a^2=(2+2i)^2=4+8i+4i^2=4+8i-4=8i
Запишем a^2 в тригонометрической форме:
a^2=8*(cos(π/2)+isin(π/2))
Решаем уравнение:
z^3=8i
Извлекаем корень кубический . Применяем формулу
( см. приложение 2)
∛(8i)=∛8*[m](cos\frac{\frac{\pi}{2}+2 \pi k}{3}+isin\frac{\frac{\pi}{2}+2\pi k}{3})[/m], k ∈ Z
при k=0
первый корень
z_(o)=2*[m](cos\frac{\pi}{6}+isin\frac{\pi}{6})=\sqrt{3}+i[/m]
при k=1
второй корень
z_(1)=2*[m](cos \frac{\frac{\pi}{2}+2\pi}{3}+isin \frac{\frac{\pi}{2}+2\pi}{3})=2\cdot (cos\frac{5\pi}{6}+isin\frac{5\pi}{6})=-\sqrt{3}+i[/m]
при k=2
третий корень
z_(2)=2*[m](cos\frac{\frac{\pi}{2}+4\pi}{3}+isin\frac{\frac{\pi}{2}+4\pi}{3})=2\cdot (cos\frac{3\pi}{2}+isin\frac{3\pi}{2})=-i[/m]
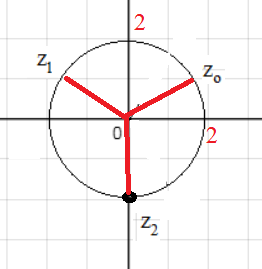
Корни расположены на окружности радиуса 2
Точки z_(o);z_(1);z_(2) делят окружность на три ( потому что корень третьей степени) равные части, каждая по 120 градусов
(cм. рис 3)