Задача 45175 Помогите решить подробно номер 12 и 13 ...
Условие
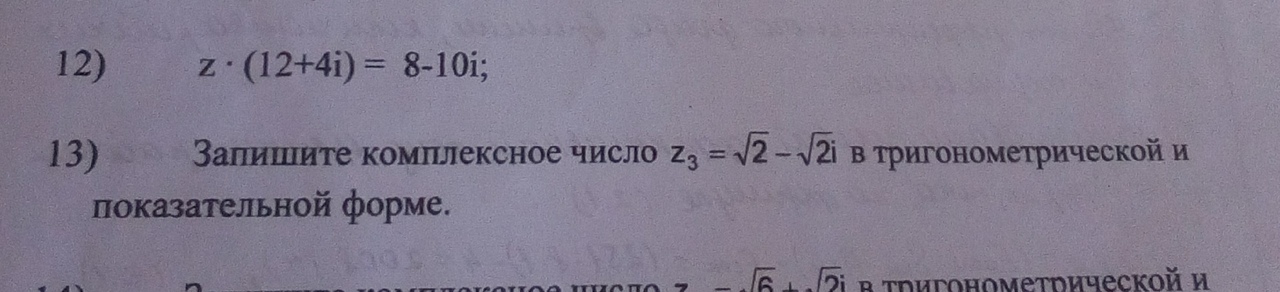
математика
769
Решение
★
Делим на 2
z*2(3+i)=4-5i
тогда
[m]z=\frac{4-5i}{2(3+i)}=[/m]
умножаем и числитель и знаменатель на (3-i)
[m]=\frac{(4-5i)(3-i)}{2(3+i)(3-i)}=\frac{12-15i-4i+15i^2}{2(3^2-(i)^2)}=
=\frac{-3-19i}{20}=-0,15-0,95\cdot i[/m]
i^2=-1
2)
|z|=sqrt((sqrt(2))^2+(-sqrt(2))^2=sqrt(4)=2
cos φ =x/|z|=sqrt(2)/2
sin φ =y/|z|=-sqrt(2)/2
⇒ φ =(-π/4)
косинус положительный, синус отрицательный, угол в 4-й четверти
z=2*(cos(-π/4)+isin(-π/4))
cos(-π/4)=cos(π/4) - в силу четности косинуса
sin(-π/4)=-sin(π/4) - в силу нечетности косинуса
z=2(cos(π/4)-i*sin(π/4)) - о т в е т
