Задача 64857 Решить уравнение: z^3 = -1 - i;...
Условие
z^3 = -1 - i;
Решение
Пусть
[m]w=-1-i[/m]
Если [m]w=x+iy [/m] ⇒ [m]|w|=\sqrt{x^2+y^2}[/m]
[m]|w|=|1-i|=\sqrt{(-1)^2+(-1)^2}=\sqrt{1+1}=\sqrt{2}[/m]
Пусть
[m]argw=\phi[/m]
[m]sin(\phi)=\frac{y}{|w|}=-\frac{1}{\sqrt{2}}[/m]
[m]cos(\phi)=\frac{x}{|w|}=-\frac{1}{\sqrt{2}}[/m]
[m]\phi=-\frac{3π}{4}[/m]
[m]w=\sqrt{2}\cdot (cos(-\frac{3π}{4})+i\cdot sin(-\frac{3π}{4}))[/m]
[m]z^3=-1-i[/m]
[m]z^3=w[/m]
[m]z=\sqrt[3]{w}[/m]
Применяем формулу Муавра (cм. приложение)
[m]z=\sqrt[3]{-1-i}[/m]
[m]z=\sqrt[3]{\sqrt{2}}\cdot (cos\frac{-\frac{3π}{4}+2πk)}{3}+i\cdot sin\frac{-\frac{3π}{4}+2πk)}{3})[/m]
k=0,1,2
при k=0
[m]z_{1}=\sqrt[3]{\sqrt{2}}\cdot (cos\frac{(-\frac{3π}{4})}{3}+i\cdot sin\frac{(-\frac{3π}{4})}{3})[/m]
при k=1
[m]z_{2}=\sqrt[3]{\sqrt{2}}\cdot (cos\frac{(-\frac{3π}{4}+2π)}{3}+i\cdot sin\frac{(-\frac{3π}{4}+2π)}{3})[/m]
при k=2
[m]z_{3}=\sqrt[3]{\sqrt{2}}\cdot (cos\frac{(-\frac{3π}{4}+4π)}{3}+i\cdot sin\frac{(-\frac{3π}{4}+4π)}{3})[/m]
Числа [m]z_{1}; z_{2};z_{3}[/m] - корни уравнения.
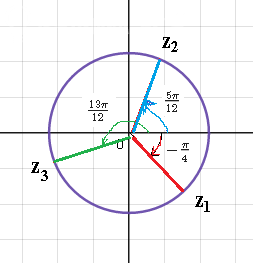
Их расположение на рисунке:
Рисуем окружность радиуса [m]\sqrt[3]{\sqrt{2}}=\sqrt[6]{2}[/m]
Откладываем луч [m]\frac{(-\frac{3π}{4})}{3}=-\frac{π}{4}[/m]
Пересечение окружности и луча - точка z_(1)
Откладываем луч [m]\frac{(-\frac{3π}{4}+2π)}{3}=\frac{5π}{12}[/m]
Пересечение окружности и луча - точка z_(2)
Откладываем луч [m]\frac{(-\frac{3π}{4}+4π)}{3}=\frac{13π}{12}[/m]
Пересечение окружности и луча - точка z_(3)
Эти три точки делят окружность на 3 равные части ( на 3 потому что корень третьей степени)