Задача 42104 ...

vk244169911

2019-11-29 18:40:15

Найти все значения ∛-8 и изобразить их на комплексной плоскости

sova

2019-11-29 19:08:18

|-8|=8
-8=8*(cosπ+i* sinπ)

Применяем формулу Муавра.

∛(-8)=∛8*[m](cos\frac{\pi+2 \pi k}{3}+isin\frac{\pi+2\pi k}{3})[/m], k ∈ Z

при k=0
первый корень
z_(o)=2*[m](cos\frac{\pi}{3}+isin\frac{\pi}{3})=1+\sqrt{3}[/m]

при k=1
второй корень
z_(1)=2*[m](cos\frac{\pi+2\pi}{3}+isin\frac{\pi+2\pi}{3})=2*(cos\pi+isin\pi)=-2[/m]

при k=2
третий корень
z_(2)=2*[m](cos\frac{\pi+4\pi}{3}+isin\frac{\pi+4\pi}{3})=2*(cos\frac{5\pi}{3}+isin\frac{5\pi}{3})=-1-\sqrt{3}[/m]

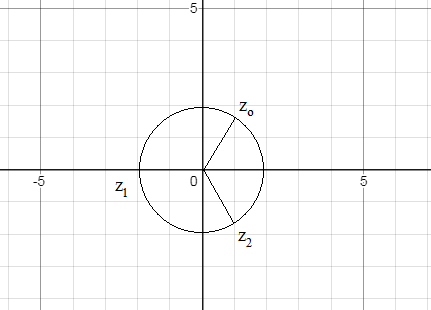
Корни расположены на окружности радиуса 2

Точки z_(o);z_(1);z_(2) делят окружность на три ( потому что корень третьей степени) равные части, каждая по 120 градусов