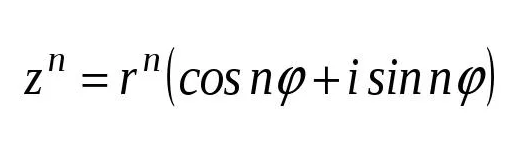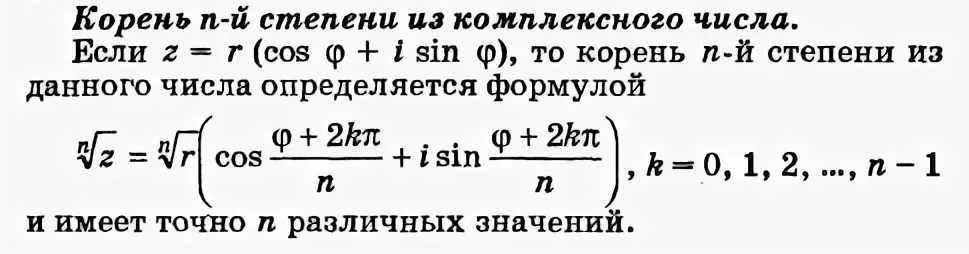Задача 60934 А) выполнить следующие действия над...
Условие
комплексными числами:
б) Решить уравнение. Корни
уравнения записать в
тригонометрической и
показательной формах. 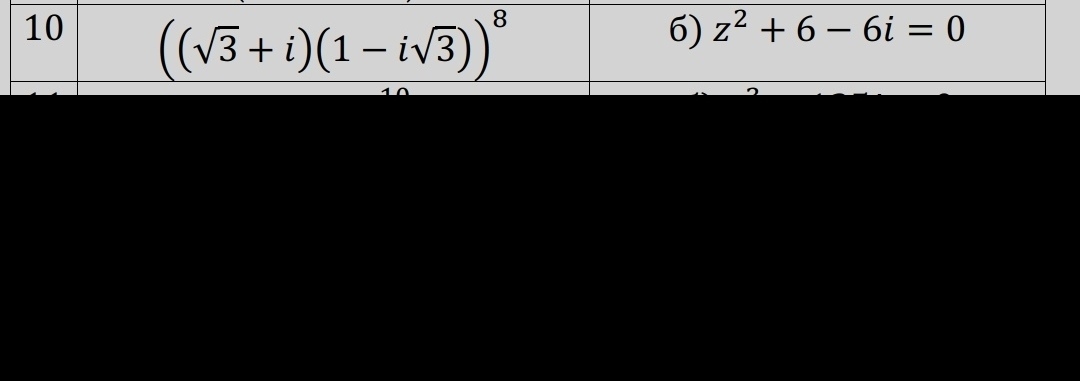
Решение
[m](\sqrt{3}+i)(1-i\sqrt{3})= \sqrt{3}+i-i\sqrt{3}\cdot \sqrt{3}-i^2\cdot \sqrt{3}=\sqrt{3}+i-3i+\sqrt{3}=2\sqrt{3}-2i[/m]
[m]((\sqrt{3}+i)(1-i\sqrt{3}))^{8}= (2\sqrt{3}-2i)^{8}[/m]
[m]z=2\sqrt{3}-2i[/m]
Представим число в тригонометрической форме и применим формулу Муавра.
z=x+i*y
|z|=sqrt(x^2+y^2)
cos φ =x/|z|
sin φ =y/z
[m]2\sqrt{3}-2i[/m]
[m]x=2sqrt{3}[/m];[m] y=-2[/m]
|z|=sqrt(2sqrt(3))^2+(-2)^2)=sqrt(12+4)=sqrt(16)=4
cos φ =x/|z|=2sqrt(3)/4=sqrt(3)/2;
sin φ =y/z=-2/4=-1/2
φ =-π/6
Значит
[m]2\sqrt{3}-2i[/m]=4(cos(-π/6)+isin(-π/6))
По формуле Муавра ( cм. скрин 1):
[m](2\sqrt{3}-2i)^{8}=4(cos(-\frac{π}{6})+isin(-\frac{π}{6}))^{8}=4^{8}\cdot (cos(8\cdot (-\frac{π}{6})+isin(8\cdot (-\frac{π}{6})=4^{8}\cdot (cos(-\frac{4π}{3})+isin(-\frac{4π}{3}))=[/m]
=[m]4^{8}\cdot (-\frac{1}{2}+i\cdot \frac{\sqrt{3}}{2})=-32768+32768\sqrt{3}\cdot i[/m]
О т в е т.
Б)
[m]z^2=-6+6i[/m]
[m]z=\sqrt{-6+6i}[/m]
Представим число [m]-6+6i[/m] в тригонометрической форме и применим формулу Муавра.
[m]-6+6i[/m]
[m]x=-6[/m];[m] y=6[/m]
[m]|-6+6i|[/m]=sqrt(-6)^2+(6)^2)=sqrt(36+36)=6sqrt(2)
cos φ =-6/6sqrt(2)=-1/sqrt(2);
sin φ =6/6sqrt(2)=1/sqrt(2);
φ =3π/4
Значит
[m]-6+6i[/m]=6sqrt(2)(cos(3π/4)+isin(3π/4))
[m]z=\sqrt{-6+6i}[/m]
[m]\sqrt[2]{-6+6i}=\sqrt[2]{6\sqrt{2}}\cdot (cos\frac{\frac{3π}{4}+2 \pi k}{2}+isin\frac{\frac{3π}{4}+2 \pi k}{2})[/m], k ∈ Z
по формуле Муавра ( cм. скрин 2)
[m]\sqrt[2]{6\sqrt{2}}=\sqrt[4]{72}[/m]
при k=0
первый корень
z_(o)[m]=\sqrt[4]{72}(cos\frac{3π}{8}+isin\frac{3π}{8})[/m]
при k=1
второй корень
z_(1)[m]=\sqrt[4]{72}(cos\frac{\frac{3π}{4}+2 \pi }{2}+isin\frac{\frac{3π}{4}+2 \pi }{2})=\sqrt[4]{72}(cos(\frac{3π}{8}+π)+isin(\frac{3π}{8}+π)[/m]
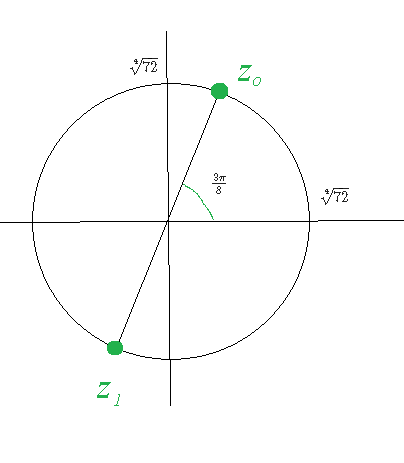
Корни расположены на окружности радиуса
[m]\sqrt[4]{72}[/m]
Точки z_(o);z_(1) делят окружность на две ( потому что корень второй степени) равные части , каждая по 180 градусов
(cм. рис )