Задача 63301 Решить вторую задачу Z = (1-i)^7 /...
Условие
Z = (1-i)^7 / (1+1)^(13)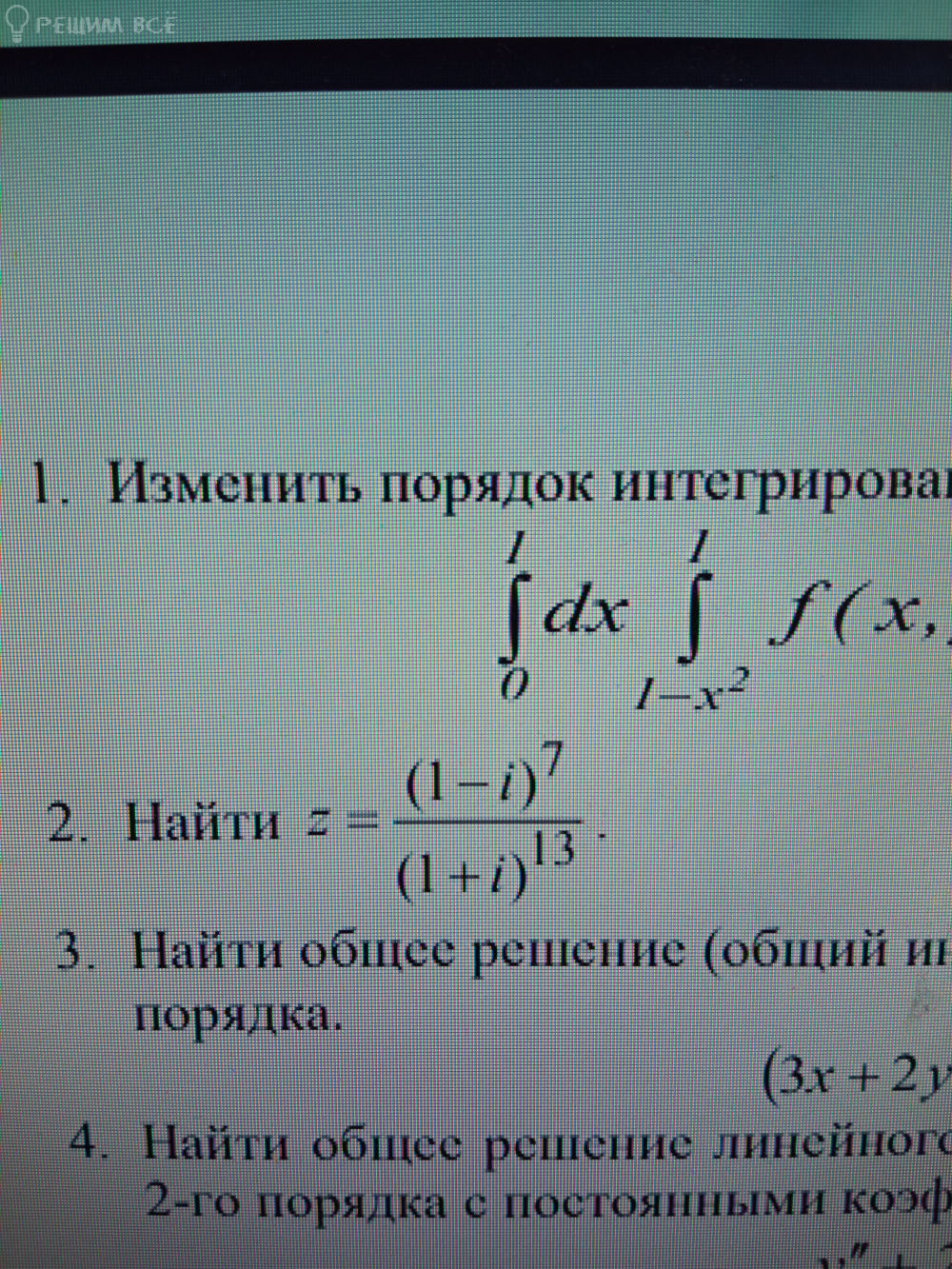
математика ВУЗ
460
Решение
★
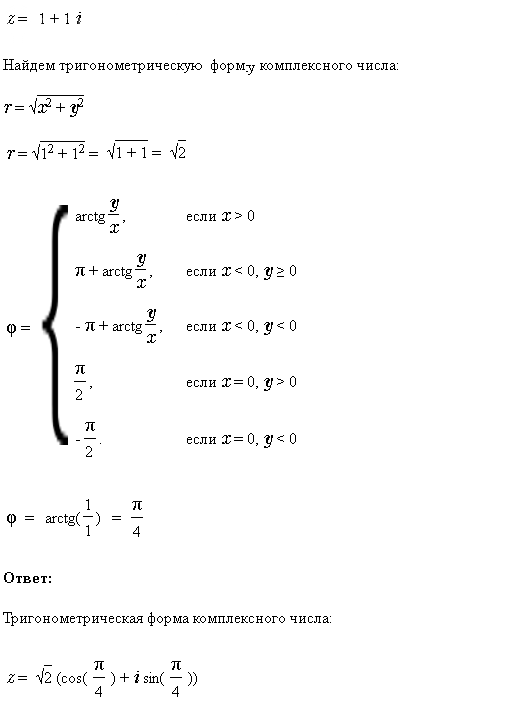
Представим число в тригонометрической форме (см. скрин 1 и 2)
1-i=sqrt(2)*(cos(-π/4)+isin(-π/4))
(1-i)^{[b]7[/b]}=(sqrt(2))^([b]7[/b])*(cos(-[b]7[/b]π/4)+isin(-[b]7[/b]π/4))=8sqrt(2)*(cos(π/4)+isin(π/4))
=8*sqrt(2)(sqrt(2)/2)+i*sqrt(2)/2)=8*(1+i)
1+i=sqrt(2)*(cos(π/4)+isin(π/4))
(1+i)^(13)=(sqrt(2))^(13)*(cos(13π/4)+isin(13π/4))=64sqrt(2)*((cos(5π/4)+isin(5π/4))=64sqrt(2)*((cos(5π/4)+isin(5π/4))=
=64sqrt(2)*(-sqrt(2)/2)-i*sqrt(2)/2)=64*(-1-i)=-64(1+i)
Теперь делим
(1-i)^(6)/(1+i)^(13)=8(1+i)/(-64*(1+i))=[b]-1/8[/b]