Задача 43634 ...

vk506281965

2020-01-23 21:19:39

Дано комплексное число a= -8/(1-i√3). Требуется: 1) записать число a в алгебраической и тригонометрической форме; 2) найти все корни уравнения
z^2=a^2. помогите пожалуйста подробно решить

sova

2020-01-23 21:35:43

★

Cначала надо избавиться от i в знаменателе.
Умножить и числитель и знаменатель
на (1+i*√3)

В знаменателе формула разности квадратов:
[green](1-i*√3)(1+i*√3)[/green]=1-(i*√3)^2=1-i^2*3=1+3=[green]4[/green]

получим

a=-8*(1+i*√3)/[green]4[/green]=2*(1+i√3=2+2i√3 - это алгебраическая форма

a=x+iy

x=2
y=2sqrt(3)

|a|=sqrt(x^2+y^2)=sqrt(2^2+(2sqrt(3))^2)=4

cos φ =x/|a|=2/4=1/2
sin φ =y/|a|=2sqrt(3)/4=sqrt(3)/2 угол в первой четверти

⇒ φ =π/3

a=4*(cos(π/3)+isin(π/3)) - тригонометрическая форма

========

a^2=(2+2isqrt(3))^2=4+8isqrt(3)-12=-8+8*isqrt(3)

Теперь для этого числа надо найти тригонометрическую форму

|a^2|=sqrt((-8)^2+(8*sqrt(3))^2)=16

cos φ =-8/16
sin φ =sqrt(3)/2 ⇒ угол во второй четверти

φ =2π/3

a^2=16*(cos(2π/3)+i*sin(2π/3))

Применяем формулу Муавра.

∛(-8+8*isqrt(3))=∛16*[m](cos\frac{\frac{2\pi}{3}+2 \pi k}{3}+isin\frac{\frac{2\pi}{3}+2\pi k}{3})[/m], k ∈ Z

при k=0
первый корень
z_(o)=∛16*[m](cos\frac{2\pi}{9}+isin\frac{2\pi}{9})=[/m]

при k=1
второй корень
z_(1)=∛16*[m](cos\frac{\frac{2\pi}{3}+2\pi}{3}+isin\frac{\frac{2\pi}{3}+2\pi}{3})=∛16(cos\frac{8\pi}{9}+isin\frac{8\pi}{9})[/m]

при k=2
третий корень
z_(2)=∛16*[m](cos\frac{\frac{2\pi}{3}+4\pi}{3}+isin\frac{\frac{2\pi}{3}+4\pi}{3})=∛16(cos\frac{14\pi}{9}+isin\frac{14\pi}{9})[/m]

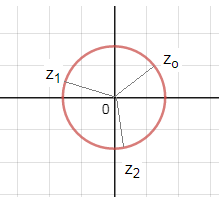
Корни расположены на окружности радиуса ∛16

Первая точка z_(o) на пересечении окружности радиуса ∛16 и радуса, образующего угол 2π/9 c осью Ох

Вторая точка z_(1) на пересечении окружности радиуса ∛16 и радиуса, образующего угол 8π/9 c осью Ох

Вторая точка z_(2) на пересечении окружности радиуса ∛16 и радиуса, образующего угол 14π/9 c осью Ох

Точки z_(o);z_(1);z_(2) делят окружность на три ( потому что корень третьей степени) равные части, каждая по 120 градусов