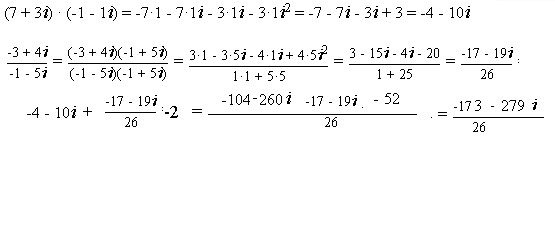Задача 60681 Комплексные числа...
Условие
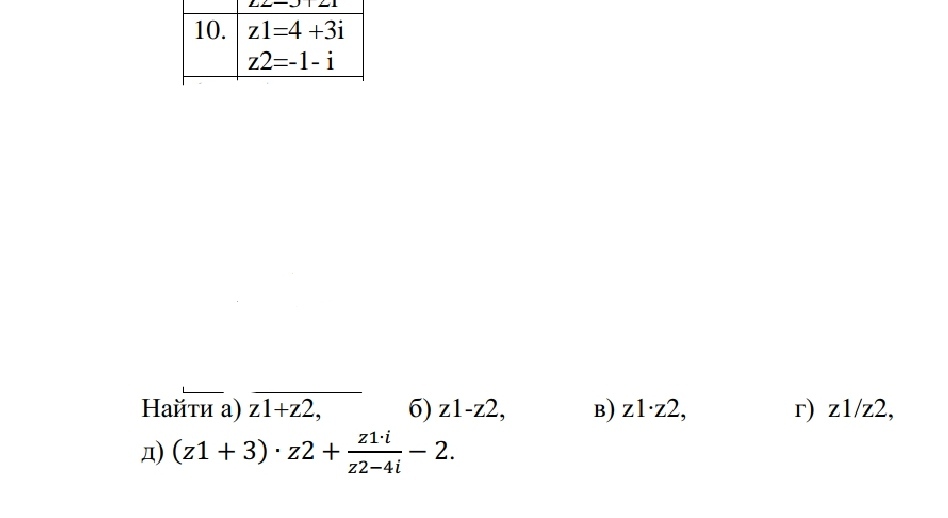
Решение
z_(1)+z_(2)=4+3*i+(-1-i)=4+3*i-1-i=[b]3+2*i[/b]
2)
z_(1)-z_(2)=4+3*i-(-1-i)=4+3*i+1+i=[b]5+4*i[/b]
3)
z_(1)*z_(2)=(4+3*i)*(-1-i)=-4-3*i-4i-3i^2=
(так как i^2=-1)
=-4-3*i-4i-3*(-1)=-4-7*i+3=[b]=-1-7*i[/b]
4)
[m]\frac {z_{1}}{z_{2}}=\frac{ 4+3\cdot i}{-1- i}=[/m]
( умножаем и числитель и знаменатель на (-1+i)
[m]=\frac{(4+3\cdot i)(-1+i)}{(-1- i)(-1+ i)}=[/m]
применяем формулу разности квадратов в знаменателе
[m]=\frac{-4-3\cdot i+4\cdot i+3\cdot i^2}{(-1)^2-(i)^2}=\frac{-4-3\cdot i+4\cdot i-3}{1-(-1)}[/m]
[m]=\frac{-7+ i}{2}[/m]
5)
[m](z_{1}+3)\cdot z_{2}+\frac{z_{1}\cdot i}{z_{2}-4i}-2=(4+3\cdot i+3)\cdot(-1- i)+\frac{(4+3\cdot i)\cdot i}{(-1- i)-4i}-2=[/m]
[m]=(7+3\cdot i)\cdot(-1- i)+\frac{4\cdot i-3}{-1- 5i}-2[/m]
Считаем по действиям
Сначала перемножим: