Задача 45406 пользуясь определением, доказать, что...
Условие
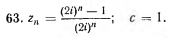
Решение
[m]|z_{n}-c|=|\frac{(2i)^{n}-1}{(2i)^{n}}-1|=|\frac{(2i)^{n}-1-(2i)^{n}}{(2i)^{n}}|=|\frac{-1}{(2i)^{n}}|=\frac{1}{2^{n}}[/m]
так как
[m]|2i|=\sqrt{0^2+2^2}=\sqrt{4}=2[/m]
[m]|2i|^{n}=2^{n}[/m]
Решаем неравенство:
[red][m]\frac{1}{2^{n}}[/m] < ε ;[/red]
[m]2^{n}>\frac{1}{ ε }[/m]
[m] n>log_{2}\frac{1}{ ε }[/m]
Поэтому достаточно взять номер n_( ε )=[[m] n>log_{2}\frac{1}{ ε }[/m]]+1
(Целой части числа [m] log_{2}\frac{1}{ ε }[/m] и с запасом +1)
А дальше все как обычно:
для любого ε > 0 найдется номер n_( ε )=[[m] log_{2}\frac{1}{ ε }[/m]]+1
такой, что для всех номер n > n_( ε )
выполняется неравенство
[m]|z_{n}-c|=\frac{1}{2^{n}}[/m] <[red] ε [/red]
(дробь в середине вообще-то не нужна, это для пояснения)
Что и означает, что limz_(n)=1 при n → ∞