Задача 33676 ...
Условие
z₁ = 4 + 3i, z₂ = 1 - √3i
Найти: ..
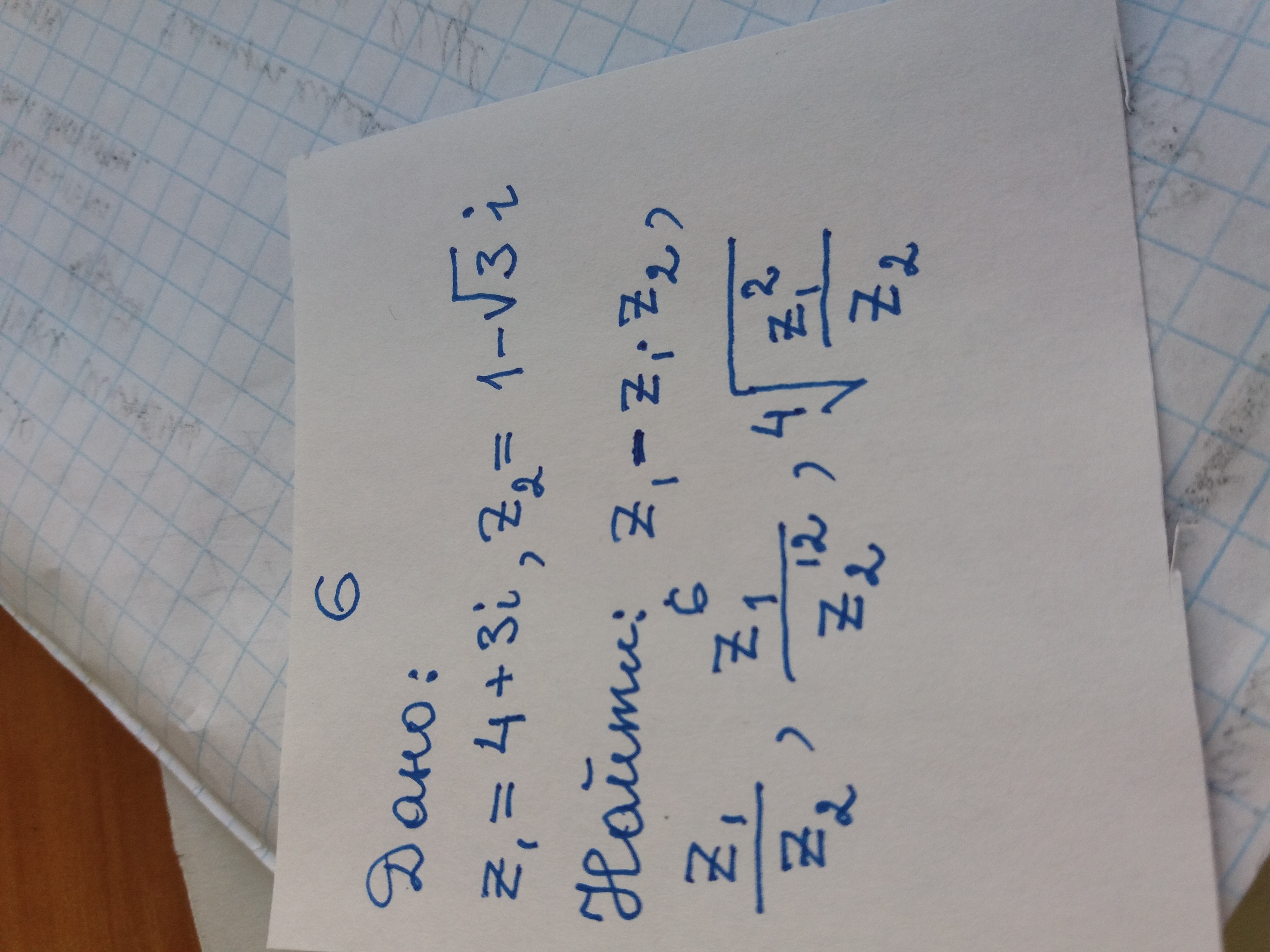
Все решения
= 4+3*i -4sqrt(3)*i -3sqrt(3)*i^2=
=(так как i^2=-1)=
= 4++3*i -4sqrt(3)*i +3sqrt(3)=
=(4+3sqrt(3))+(3-4sqrt(3))*i
z_(1)- z_(1)*z_(2)= (4+3*i) - (4+3sqrt(3))-(3-4sqrt(3))*i=
=[b] -3*sqrt(3) +4sqrt(3)*i [/b]
2) z_(1)/z_(2)=( 4 + 3i)/(1 -sqrt(3) *i)
( умножаем и числитель и знаменатель на (1+sqrt(3)*i))
=( 4 + 3i)(1+sqrt(3)*i)/((1 -sqrt(3) *i)(1+sqrt(3)*i))
=(4+3*i+4sqrt(3)*i+3sqrt(3)*i^2)/(1 -(sqrt(3))^2* i^2)=
=((4-3sqrt(3)) +(3+4sqrt(3))*)/(4)=
=[b](1/4)*(4-3sqrt(3)) + (1/4)*(3+4sqrt(3))*i[/b]
3)
z^6_(1)=(4+3*i)^6=((4+3*i)^2)^(3)=(7+24*i)^3=
можно возвести в куб по формуле (a+b)^3
=7^3+3*7^2*24*i-3*7*24^2-24^3*i
z^(12)_(2)=(1-sqrt(3)*i)^(12)
Запишем z_(2) в тригонометрической форме и применим формулу Муавра
( см. приложение)
z_(2)=(1-sqrt(3)*i)
|z_(2)|=sqrt(1^2+(-sqrt(3))^2)=sqrt(1+3)=sqrt(4)=2
argz_(2)=phi
sin(phi)=y/|z_(2)|=-sqrt(3)/2
cos(phi)=x/|z_(2))=1/2
phi=(-π/3)
z_(2)=2*(cos(-π/3)+i*sin(-π/3))
z^(12)_(2)=2^(12)*(cos(-π/3)*12+i*sin(-π/3)*12)=
=2^(12)*(cos(-4π)+i*sin(-4π))=
=2^(12)
z^6_(1)/z^(12)_(2)=((7^3-3*7*24)+(3*7^2*24-24^3)*i )/ 2^(12)
можно упростить.
4)
z_(1)=(4+3*i)
z^(2)_(1)=(4+3*i)*(4+3*i)=16+24*i-9=7+24*i
z_(3)=z^(2)_(1)/z_(2)=(7+24*i)/(1-sqrt(3)*i)=(7+24*i)(1+sqrt(3)*i)/4=
=(7+24*i+7sqrt(3)*i-24sqrt(3))/4=
=(7-24sqrt(3))+(24+7sqrt(3))*i
|z_(3)|=sqrt((7-24sqrt(3))^2+(24+7sqrt(3))^2)=
=sqrt(49-7*48*sqrt(3)+576*3+576-7*48sqrt(3)+49*3)=
=sqrt(49*4+576*4)=2*sqrt(49+576)=2*sqrt(625)=2*25=50
argz_(3)=phi
sin(phi)=y/|z_(3))=(24+7sqrt(3))/50
cos(phi)=x/|z_(2))=(7-24sqrt(3))/50
tg(phi)=(24+7sqrt(3))/(7-24sqrt(3))
???
Извлечь корень 4-ой степени можно по формуле извлечения корней, но аргумент не найден
