Задача 30281 ...

vk344135258

2018-10-17 16:25:11

Даны комплексные числа z1 и z2 в алгебраической форме. Требуется: 1) представить z1 и z2 в тригонометрической форме; 2) найти: а) z1^3 * z2^4 ; б) z1^5 / z2^3 ; в) 4√z2 и построить.

5. z1 = -2 + 2√3i ; z2 = 1 - i

sova

2018-10-17 18:02:10

★

z_(1)=(-2+2sqrt(3)*i)

|z_(1)|=sqrt((-2)^2+(2sqrt(3))^2)=sqrt(4+12)=sqrt(16)=4
argz_(1)=phi

sin(phi)=y/|z_(1)|=2sqrt(3)/4=sqrt(3)/2
cos(phi)=x/|z_(1))=-2/4=-1/2
phi=2π/3

z_(1)=4*(cos(2π/3)+i*sin(2π/3))

Аналогично

|z_(2)|=sqrt(1^2+(-1)^2)=sqrt(2)

argz_(2)=ψ

sinψ=y/|z_(2)|=-1/sqrt(2)
cosψ=x/|z_(2))=1/sqrt(2)
ψ=-3π/4

z_(2)=sqrt(2)*(cos(-3π/4)+i*sin(-3π/4))

так как
cos(-3π/4)=cos(3π/4)
sin(-3π/4) = - sin(3π/4)

z_(2)=sqrt(2)*(cos(3π/4)-i*sin(3π/4))


Применяем формулу Муавра (cм. приложение)
a)
z^(3)_(1)=4^3(cos3*(2π/3)+i*sin3*(2π/3))= 64*(cos2π+i*sin2π)=64
z^(4)_(2)=(sqrt(2))^4*((cos4*(3π/4)-i*sin4*(3π/4))=
=4*(cos3π-i*sin(3π)= - 4

z^(3)_(1)*z^(4)_(2)=64*(-4)=-256

б)
z^(5)_(1)=4^5(cos5*(2π/3)+i*sin5*(2π/3))=
=1024*(cos(10π/3)+i*sin(10π/3))=
=1024*((-1/2)+i*(-sqrt(3)/2)=-512-i*512sqrt(3)

z^(3)_(2)=(sqrt(2))^3*((cos3*(3π/4)-i*sin3*(3π/4))=
= 2sqrt(2)(cos(9π/4)-i*sin(9π/4)= 2sqrt(2)*(-sqrt(2)/2)-i*(-sqrt(2)/2)=
= - 4+4*i

z^(5)_(1)/z^(3)_(2)=(-512-i*512sqrt(3))/(-4+4*i)=

сокращаем на 4 и умножаем и числитель и знаменатель на
(-1-i )

=(-128-i*128sqrt(3))*(-1-i)/(1+1)=

=(64 + 64sqrt(3))+(64+64sqrt(3))*i

в)

z^(1/4)_(2)=(sqrt(2))^(1/4)*cos(((-3π/4)/4)+(πk/2))+i*sin(cos(((-3π/4)/4)+(πk/2))

k=0,1,2,3

при k=0
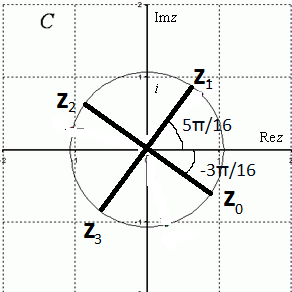
(z^(1/4)_(2))_(0)=2^(1/8)*(cos(3π/16)+i*sin(-3π/16))

при k=1
(z^(1/4)_(2))_(1)=2^(1/8)*(cos(5π/16)+i*sin(5π/16))

при k=2
(z^(1/4)_(2))_(2)=2^(1/8)*(cos(13π/16)+i*sin(13π/16))

при k=3
(z^(1/4)_(2))_(2)=2^(1/8)*(cos(21π/16)+i*sin(21π/16))

4 числа, которые являются ответом.
См их расположение на рисунке.