Задача 56148 ...
Условие
Помогите пожалуйста! Перевести в алгебраическую форму и решить (1+i)^8(1-√3i)^6
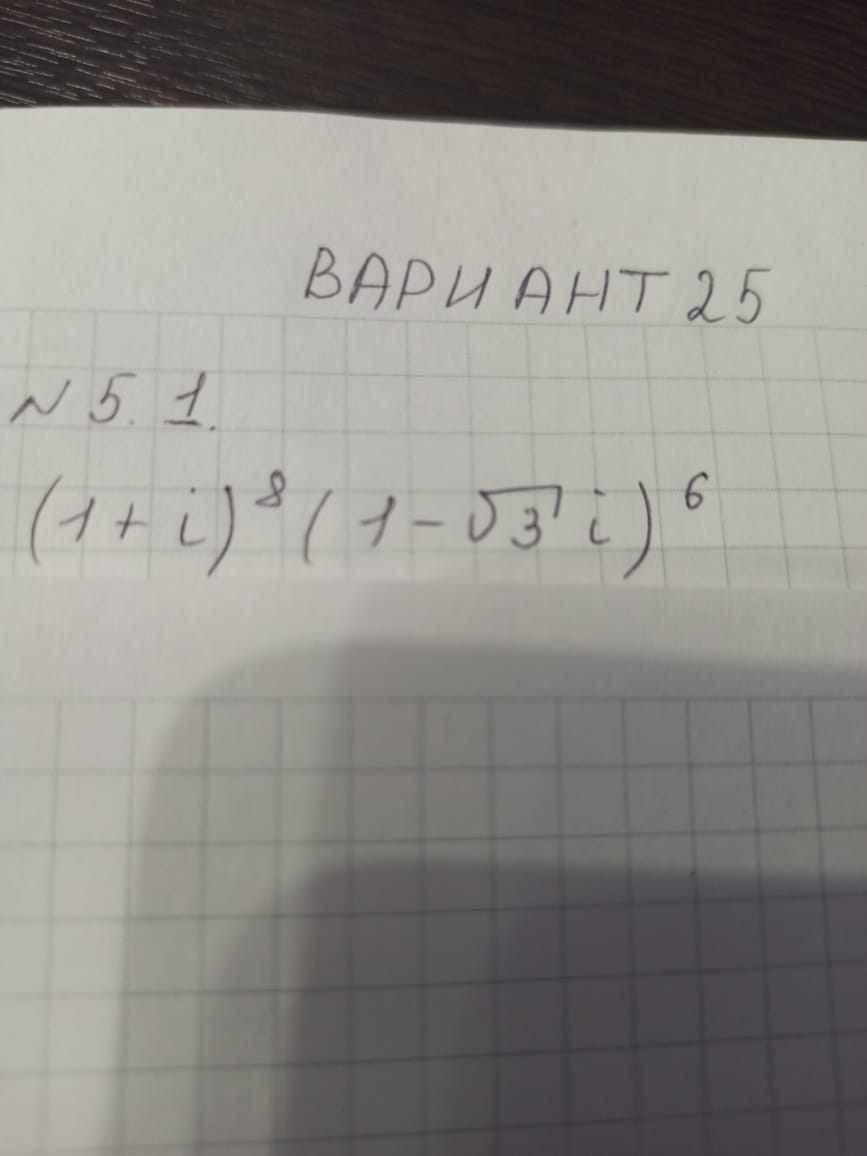
математика ВУЗ
1036
Решение
★
|z|=sqrt(x^2+y^2)
cos φ =x/|z|
sin φ =y/z
z=1+i
x=1; y=1
|z|=sqrt(1^2+1^2)=sqrt(2)
cos φ =x/|z|=1/sqrt(2)
sin φ =y/z=1/sqrt(2)
φ =π/4
Значит
1+i=sqrt(2)*(cos(π/4)+isin(π/4))
По формуле Муавра:
(1+i)^8=(sqrt(2))^8*(cos(8*(π/4))+isin(8*(π/4))=16*(cos2π+isin2π)=16*(1+i*0)=[b]16[/b]
Аналогично
z=1-sqrt(3) * i
x=1
y=-sqrt(3)
|z|=2
cos φ =x/|z|=1/2
sin φ =y/z=-sqrt(3)/2
φ =-π/6
1-sqrt(3) * i=2*(cos(-π/6)+isin(-π/6))
По формуле Муавра:
(1-sqrt(3) * i)^6=2^6*(cos6*(-π/6)+isin6*(-π/6))=64*(cos(-π+i*sin(-π))=64*(-1)[b]=-64[/b]
О т в е т. 16*(-64)=...