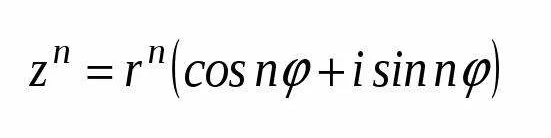Задача 63302 Решить вторую задачу Z = (sqrt(3)/3 +...
Условие
Z = (sqrt(3)/3 + sqrt(3)/3 I)^(100) 
Решение
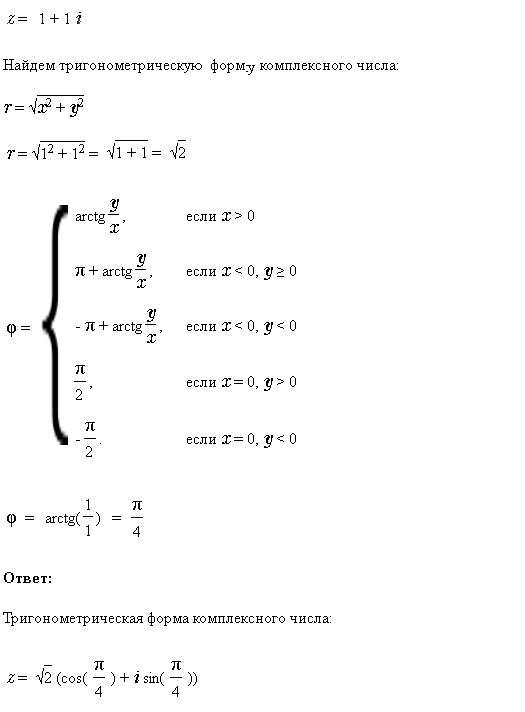
Представим комплексное число [m]1+i[/m] в тригонометрической форме
[m]1+i=\sqrt{2}(cos\frac{π}{4}+isin\frac{π}{4})[/m]
Применяем формулу Муавра
[m] (1+i)^{100}=(\sqrt{2}(cos\frac{π}{4}+isin\frac{π}{4}))^{100}=2^{50}\cdot (cos\frac{100π}{4}+isin\frac{100π}{4})=[/m]
[m]=2^{50}\cdot (cos 25 π+isin 25 π)=2^{50}\cdot (cos (24 π+π)+isin (24 π+π))=2^{50}\cdot (cosπ+isinπ)=2^{50}\cdot (-1+i\cdot 0)=-2^{50}[/m]
[m](\frac{\sqrt{3}}{3}+i\cdot\frac{\sqrt{3}}{3})^{100}=( \frac{\sqrt{3}}{3})^{100}\cdot (1+i)^{100}=\frac{3^{50}}{3^{100}}\cdot (-2^{50})=-\frac{2^{50}}{3^{50}}[/m]