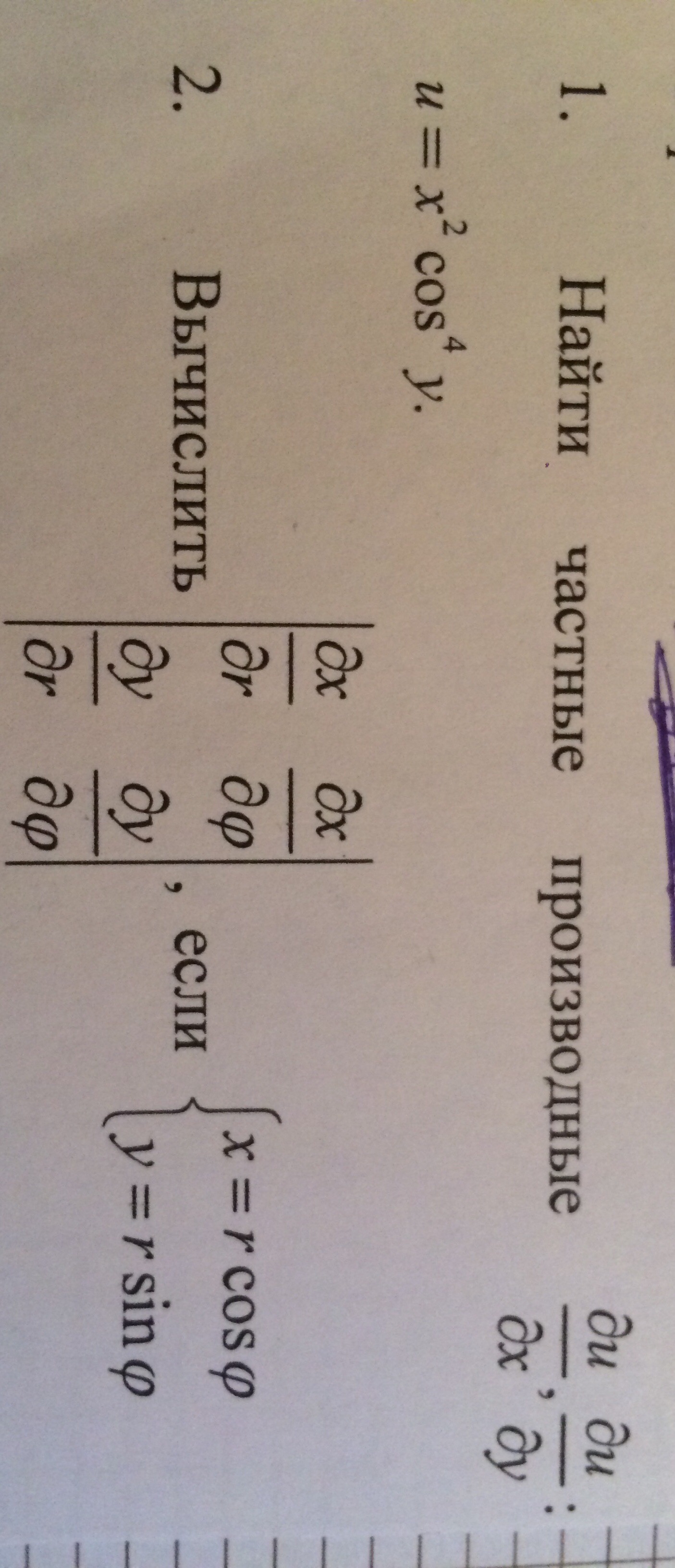
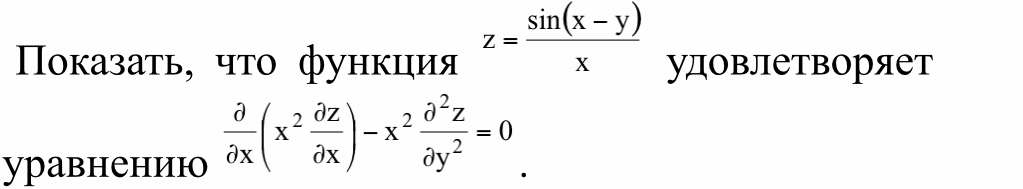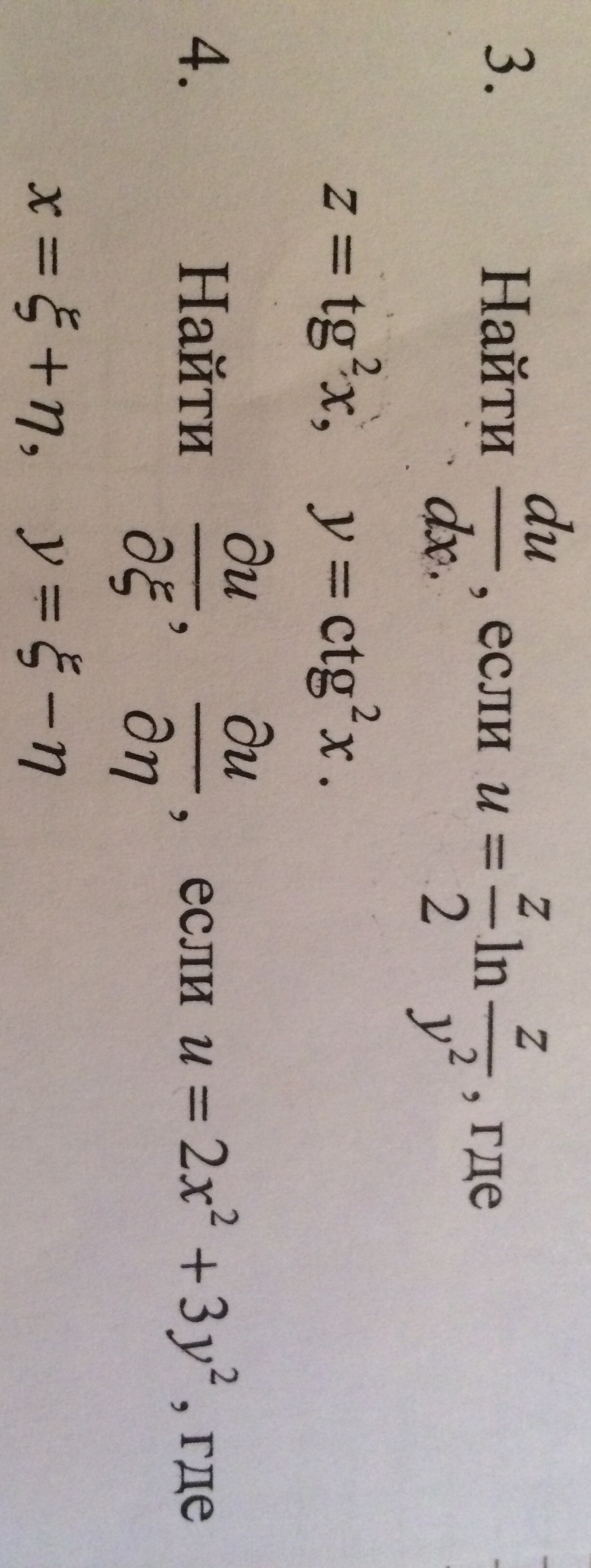Частные производные и дифференциалы

2. Дифференциальные исчисление функций нескольких переменных

231. Дана функция z = e^(xy). Показать, что x^2 d^2z/dx^2 - y^2 d^2z/dy^2 = 0.

Вычислить значения частных производных функции ???? = ????(????, ????), заданной неявно:
????^3 + 2????^3 + ????^3 − 3???????????? − 2???? − 15 = 0, в данной точке ????0 (1; −1; 2) с точностью до двух знаков после запятой. +общую формулу част. производных

Как дальше делать. Делал всё как в примере, у меня отличается лишь значения точки(1÷2, sqrt(3)÷2) и аргумент x у меня убывает.
Я остановился на пункте, где находят значение угла альфа и бетта
Вот пример с которого я делал https://reshimvse.com/zadacha.php?id=33901

Найти частные производные данной функции по каждой из независимых переменных (x,y) и полный дифференциал

z=ln(x^-y+ln y)

Найти градиент функции u=u(x,y,z) и ее производную в точке P(x0,y0,z0)в направлении вектора PP1.
u=x sinz+e^y P0(1;0;0) P1(0;2;2)

z=tg(x-y)/x Показать, что ∂^2z / ∂x∂y + ∂^2z / ∂y^2 + 1 / x ∂z / ∂y = 0.

Найдите производную функции f(x, y, z) = z^3 - x^2*y в точке (-5, -5, -5) по направлению v = (-3, 2, 5).

Найти частные производные от функций

z = e^(xy)(ln(x + y))

Найти частные производные от функций

u = x^(yz)

Найти полные дифференциалы функций

z = ln(tg(x + y)/(x - y))

Найти полные дифференциалы функций

z = x / sqrt(x² + y²)

4.Найти полные дифференциалы функций

z = arctg y/x + arctg x/y

Дано скалярное поле u=u(x;y)
а)Составить уравнение линии уровня u=C и построить график.
б) вычислить с помощью градиента производную скалярного поля u=u(x;y) в точке А по направлению вектора АВ.
x^2+y^2-2x+2y C=2 A(1,5;-1- (sqrt3)/2 B(0;-1-(sqrt3)/2
Вариант 6 на фотографиии

Найдите градиент функции z  f x, y в точке A.
Найдите производную функции z  f x, y в точке A по направлению вектора АВ . Z=2x^(2)+xy/ A(-1:2) B(2:6)

хелп, нужна помощь с вычислением приближенного значения, пример прилагаю

Найти производную функции u в точке М по направлению, идущему от этой точки к точке P. u = xz4/y + xzy5 + y/z2; M(1, 1, -1); P(3, -5, 2)

Найти производную функции u = z/x2 + xy3+ yz5 в точке M(1,1,1) по направлению, идущему от этой точки к точке P(2,5,9)
Найти направляющие косинусы вектора MP и значение производной по направлению (например, cosα=2/7, cosβ=3/7, cosγ=6/7; ∂u/∂MP=15/7

Найти Z’_(x) и Z’_(y) если Z=ln(x^2 + y^4)

Найти для функции u=7x^2y-3xz^2+5yz^2 производную по направлению n={-12,0,5} в точке М(2,1,-1).

Дана функция z=f(x,y). Найти:
1)полный дифференциал dz
2)частные производные второго порядка
z=tgx/y

[red]Даны: функция z=f(x,y), точка A и вектор a . Требуется найти: 1) grad z в точке A ; 2) производную в точке A по направлению вектора a ; 3) экстремум функции z=f(x,y)[/red]

Найти частные производные dz/dx,dz/dy от функции z=z(x,y)

Найти полный дифференциал функции . z=exp(xy)

Вычислить приближенные значения данных функций в точке (x0,y0), используя формулу Тейлора с n=2.

Нужно решить номер 112,122
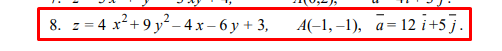
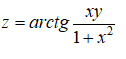
В 112 номере найти полный дифференциал функции (функция указана на фото)
В 122 номере найти экстремумы функций

Нужно ли делать замену по x и y везде ? Или только в dz/dt

Найти dx/dt, если \( z = z(x;y) \), \( x = x(t) \), \( y = y(t) \):

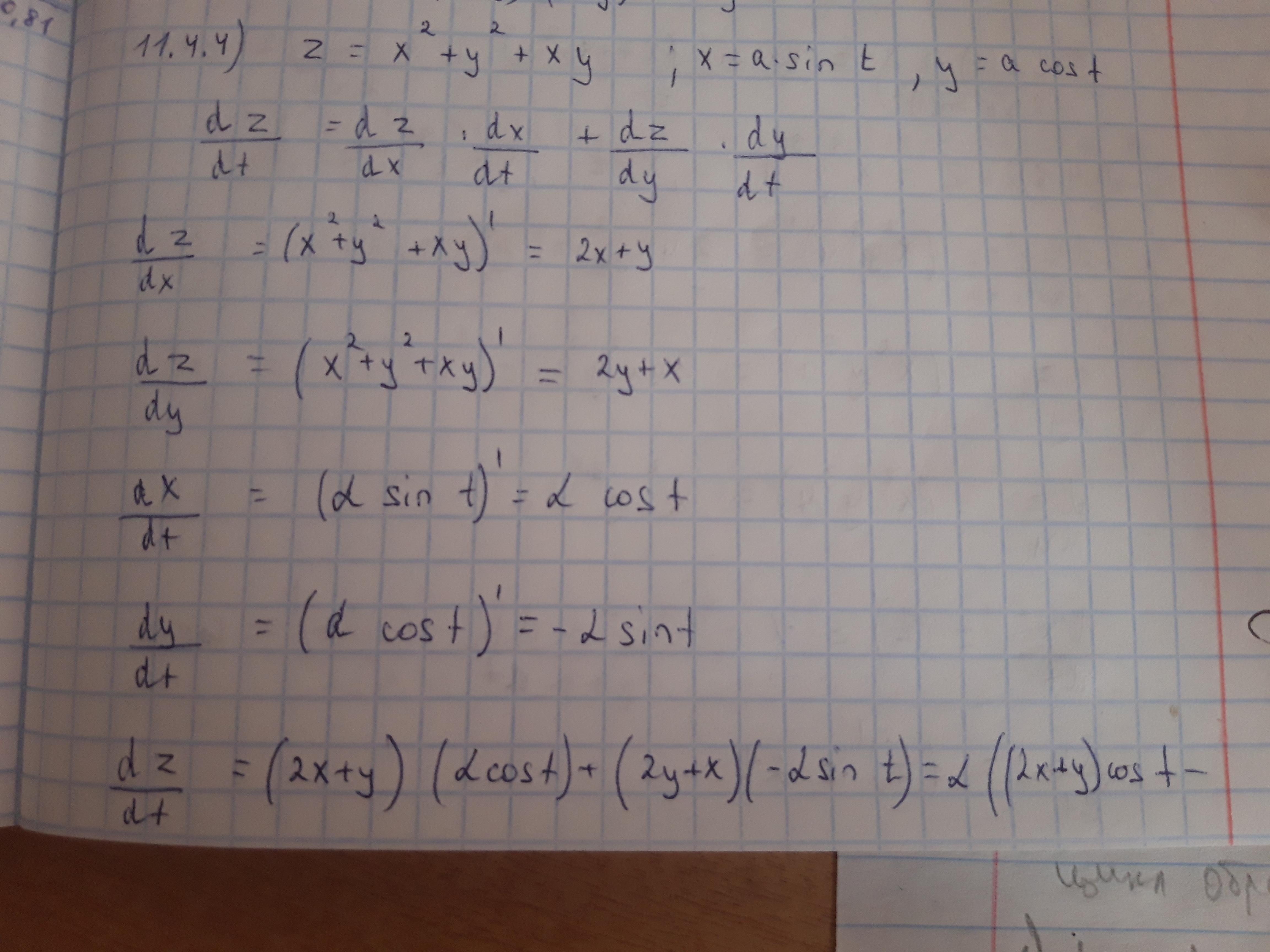
11.4.4. \( z = x^2 + y^2 + xy \), \( x = a \sin t \), \( y = a \cos t \).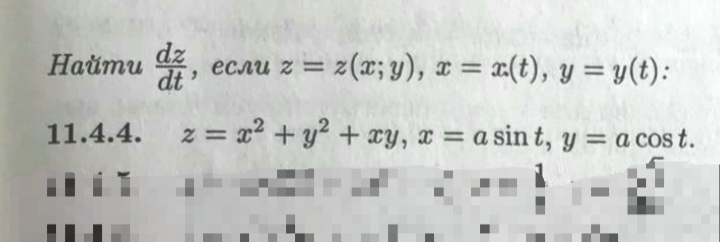

4. Вычислить все частные производные второго порядка для функции
[m] u = \frac{1}{2}\sin^2 ( 1 - xyz ) + \frac{x}{y - 3z}. [/m]

5. Вычислить дифференциал [m] d^3 u [/m] для функции [m] u = \frac{y}{x} + x^4 \sqrt{y}. [/m]

∂f / ∂s z = 2r٫ y = r² + Ln(s) ⋅ x = r/s ⋅ f(x, y, z) = x + 2y + z²

11.5.19 \\ Найти dz u d2 z от следующих :z=(x2+y2)3

Дана функция z = x^y. Найти ∂z/∂x,∂z/∂y ,∂^2z/∂x^2,∂^2z/∂y^2,∂^2z/∂x∂y.

2. Оценить абсолютную и относительную погрешности при вычислении значения функции z = √2x + y², при x = 2 ± 0,01, y = 4 ± 0,02.

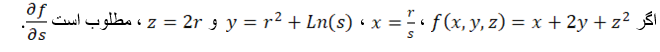
3. Написать формулы для производных ∂u/∂t и ∂u/∂s для функции
u = (1/3)^(x-2x) + cos((y + x)/2z), при x = x(s), y = y(t,s), z = z(t,s).

Вычислить приближенно:

Найти ∂z/ ∂x, ∂z/ ∂y для неявных функций z=z(x;y), определяемых следующими уравнениями:

Найти dz и d^(2)z от следующих функций:

Пожалуйста помогите. Найти полный дифференциал функции

6.3. Найти значение производной от функции f(x)= sin (cos x )+4x^3 в точке с координатой x= 1.

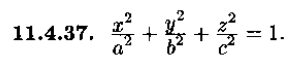
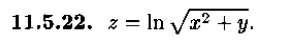
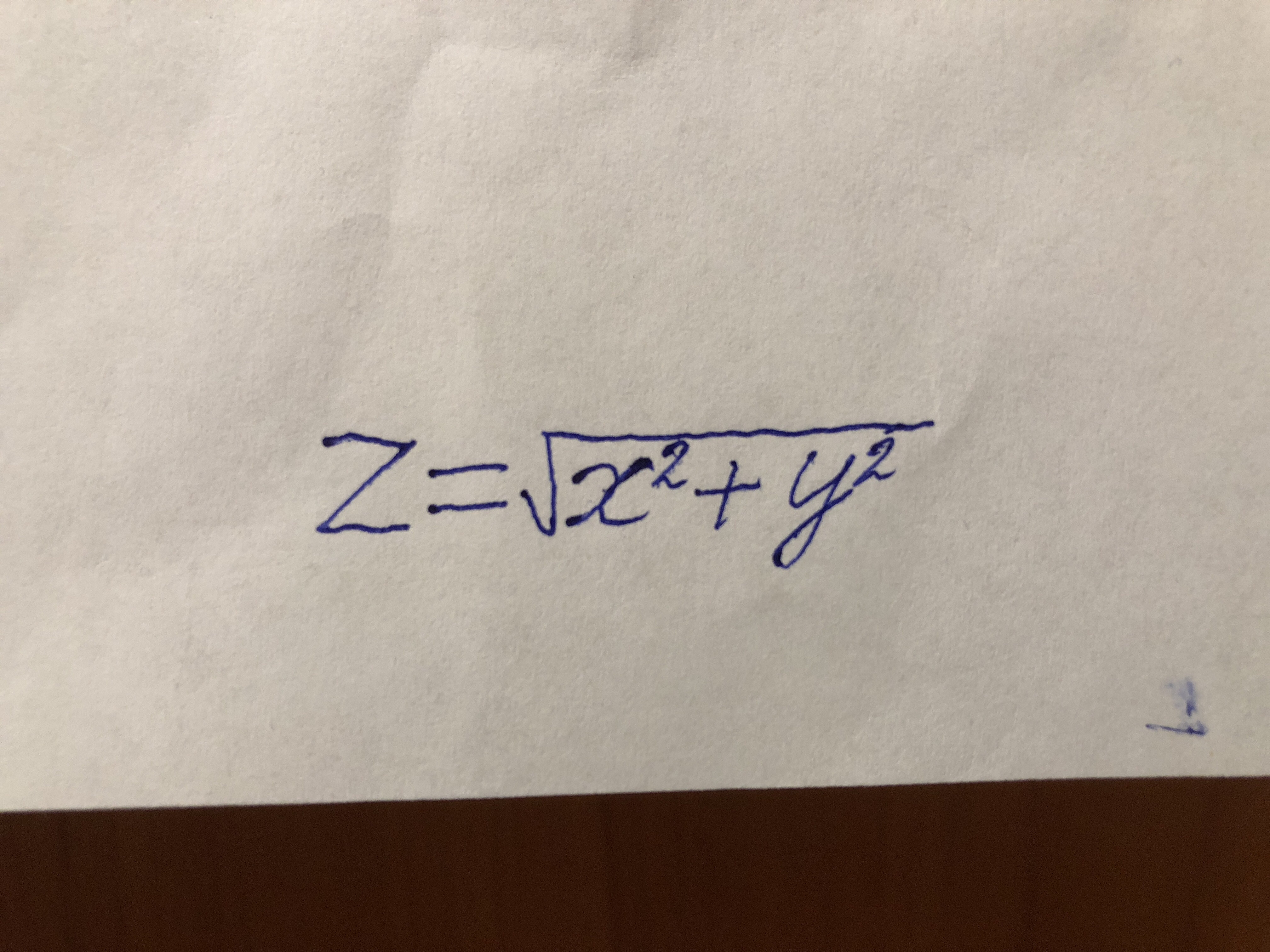
6.4. Найти частные производные z’x и z’y функцши z= ln(x^2+y)

6.5. Найти градиент функции U=f(x,y,z) в точке M.
U =ln(3 - x^2 ) +x y^z^2 M ( 1, 3, 2)

1) z=x^2+2xy+y^2+x^3-3x^2y-y^3+x^4-4x^2y^2+y^4 2) z=x^2y^2

1. Найти частные производные второго порядка: z = (y-2)/x^2.

2. Найти экстремумы функции двух переменных:
z = 2x^3 + 6xy^2 - 30x - 24y + 9.

3. Найти указанные производные z = 3x^3 + xy^2 - 5xy^3 - 2x + y, ∂4z ∂x∂y3 = ?

4. Найти наибольшее и наименьшее значения функции z = x2 - xy + y2 - 4x в треугольнике x = 0, y = 0, 2x + 3y - 12 = 0.

5. Найти точку пересечения прямой и плоскости
x-5 -2 y-2 0 z+4 -1 2x - 5y + 4z + 24 = 0.

Помогите решить как можно быстрее пожалуйста

Помогите решить пожалуйста..только 8 пример

Определить градиент и производную заданной функции z = arctg(y/x) в т M0(1,1) в направлении линии х^2+ у^2 = 2х в сторону возрастания аргумента х.

Срочно!!!
Минут 40 осталось

Помогите решат задачу Спасибо

2. Найти частные производные ∂z/∂x, ∂z/∂y от неявной функции zln(x+z)=xy/z

Вычислить производную сложной функции. 17-ый пример!

Найти производную функции u=xz^4/y+xzy^5+y/z^2 в точке М (1,1,-1) по направлению идущему от этой точки к точке Р(3,-5,2). Направляющие косинусы вектора MP и значение производной по направлению.

5.22 Найти производную функции  в точке  в направлении, идущем от этой точки к точке . Смотреть фото.

Найти производную функции f(x, y) = (10 + 4x⁻² - 3y³ - x³y³)²
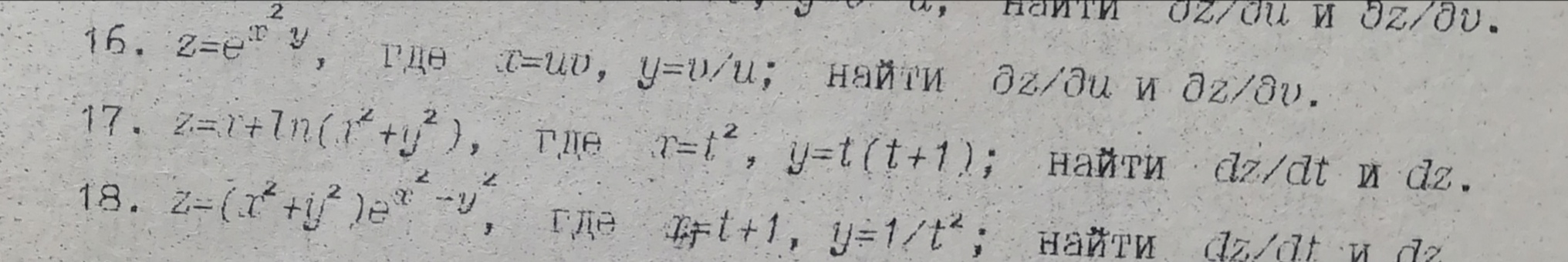
в точке K(1, 1) по направлению к точке M(4, 6).

d^2u/dx^2+d^2u/dy^2+d^2u/dz^2=0,u=1/sqrt(x^2+y^2+z^2)
Данное уравнение данной функции u должно быть выполнено.

z=arctg(x-3y) найти вторые частные производные функции

Показать, что функция удовлетворяет уравнению
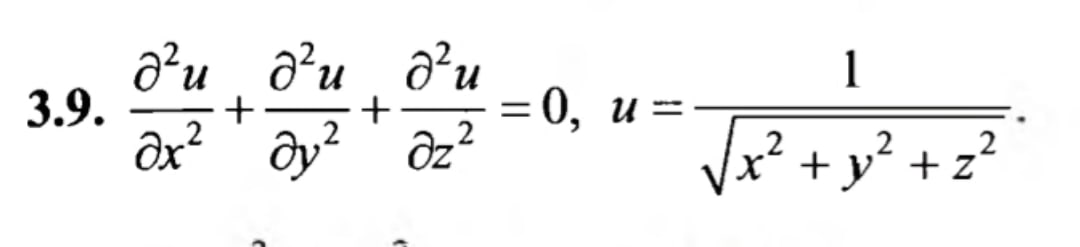
Фото)