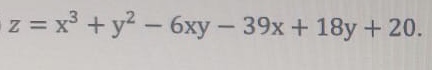Исследование на экстремум

Найти локальные безусловные экстремумы функции

u = y^zx2

исследовать на экстремум функцию: z=–2x³–3y²–6xy–12x–12y

Нужно решить номер 112,122
В 112 номере найти полный дифференциал функции (функция указана на фото)
В 122 номере найти экстремумы функций

Найти стационарные точки и исследовать на экстремум данные функции:

f(x; y) = 4x² – 5xy + 3y² – 9x –8y.

Найти стационарные точки и исследовать на экстремум данные функции:

Задача 5. Найти наибольшее и наименьшее значения функции
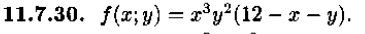
области D, ограниченной заданными линиями.

5.7. z = 2x³ – xy² + y², D: x = 0, x = 1, y = 0, y = 6.

Найти наибольшее и наименьшее значение функции z=3x²+3y²–2x–2y+2 в области D: y+x–1=0, y=0, x=0

1. Найти частные производные второго порядка: z = (y–2)/x².

2. Найти экстремумы функции двух переменных:
z = 2x³ + 6xy² – 30x – 24y + 9.

3. Найти указанные производные z = 3x³ + xy² – 5xy³ – 2x + y, ∂4z ∂x∂y3 = ?

4. Найти наибольшее и наименьшее значения функции z = x2 – xy + y2 – 4x в треугольнике x = 0, y = 0, 2x + 3y – 12 = 0.

5. Найти точку пересечения прямой и плоскости
x–5 –2 y–2 0 z+4 –1 2x – 5y + 4z + 24 = 0.

Помогите решить как можно быстрее пожалуйста

Задание 6. Исследовать функцию двух переменных на экстремум.

8. [m] z = 2x^2 + y^2 - xy + 2x + 3y - 7 [/m]

Найти наименьшее и наибольшее значения
функции
z = f (x, y) в замкнутой области D , заданной системой неравенств. Сделать
чертеж.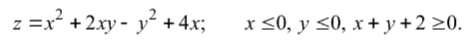

Найдите наибольшее и наименьшее значение функции z=xy–x–2y в области D:y=x, y=0, x=3

Исследовать на экстремум функцию z = f (x,y)
z=8x–4y+x²–xy+y²+15

помогите решить задание по шаблону

Исследовать на экстремум функцию z=x³+8y³–6xy+5

Исследуйте на экстремум функцию

z = x³ + y² – 6xy – 39x + 18y + 20.

.Здравствуйте. Помогите решить задачу. Найти наименьшее и наибольшее значения функции z=x²+2y²+1 в замкнутой области D, заданной системой неравенств x≥ 0, y≥ 1, x+y≤3. Сделать чертеж.

Найти точки экстремума функции двух переменных и исследовать их характер
Фото)