Задача 45318 ...

vk139970910

2020-03-25 14:01:18

.Здравствуйте. Помогите решить задачу. Найти наименьшее и наибольшее значения функции z=x^2+2y^2+1 в замкнутой области D, заданной системой неравенств x≥ 0, y≥ 1, x+y≤3. Сделать чертеж.

sova

2020-03-25 14:04:40

Находим частные производные:
z`_(x)=2x
z`_(y)=4y

Находим стационарные точки:
{z`_(x)=0
{z`_(y)=0

{2x=0 ⇒ х=0
{4y=0 ⇒ у=0

(0;0) - стационарная точка

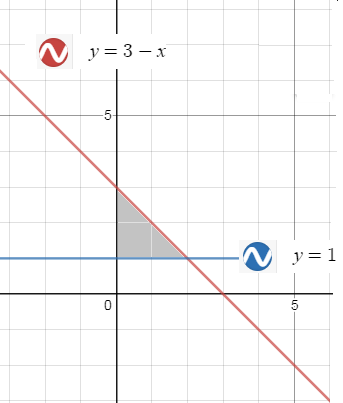
Рисуем область
(0;0) - стационарная точка этой области не принадлежит.

Значит, наибольшее и наименьшие значения функция принимает на границах области.

[b]y=1[/b]
z=x^2+2*1^2+1
z=x^2+3 - парабола на [0;2] cм рис. y=1 рассматривается при
0 ≤ х ≤ 2
Парабола возрастает, z`=2x>0 при любом х ∈ [0;2] ⇒
При х=0 наименьшее [b]z=3[/b]
При х=2 наибольшее [b]z=7[/b]

[b]x=0[/b]
z=0^2+2*y^2+1
z=2y^2+1 - парабола на [1;3] cм рис.
прямая x=1 рассматривается при
1 ≤ х ≤ 3
Парабола возрастает, z`=4y>0 при любом y ∈ [1;3] ⇒
При y=1 [b]z=3[/b]
При y=3 [b]z=2*3^2+1; z(0;3)=19[/b]

x+y=3 ⇒ x=3-y
z=(3-y)^2+2*y^2+1
z=3y^2-6y+10 - парабола на [0;2] cм рис.
отрезок прямой x+y=3 при
0 ≤ х ≤ 2
z`=6y-6
z`=0
y=1 ⇒ x=2
z(2;1)=7
При х=0 ⇒ y=3 [b]z(0;3)=19[/b]
При х=2 ⇒ y= 1 [b]z=7[/b]

Выбираем наибольшее и наименьшее
z_(наибольшее)=[b]19[/b]
z_(наименьшее)=[b]3[/b]