Задача 33830 Найдите наибольшее и наименьшее значение...
Условие
Решение
z`_(y)=x-2
Находим стационарные точки
{z`_(x)=0
{z`_(y)=0
{y-1=0
{x-2=0
Получили одну стационарную точку.
Применяем теорему: достаточное условие существования точек экстремума.
Находим вторые частные производные
z``_(xx)=0
z``_(xy)=1
z``_(yy)=0
Значения в стационарной точке
(2;1)
A=z``_(xx)(2;1)=0
C=z``_(xy)(2;1)=1
B=z``_(yy)(2;1)=0
Δ(2;1)=AB-C^2=0*0-1^2 < 0
Точка (2;1) не является ни точкой максимума, ни точкой минимума.
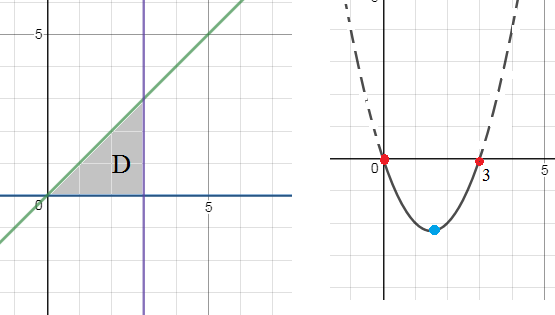
Исследуем функцию на границе:
[b]при y=x[/b]
z=x^2-3x
Это функция одной переменной, исследуем ее как обычную параболу
при 0 ≤ x ≤ 3
При х=0 и х=3 функция принимает наибольшее значение
При х=3/2 функция принимает наименьшее значение
При х=0; y=0
z(0;0)=0
При x=3; y=3
z(3;3)=3*3-3-2*3=0
Если поверхность z=xy-x-2y разрезать по прямой y=x, то на срезе будет
часть параболы как на рис. справа
[b]при y=0[/b]
z=-x - как функция одной переменной на [0;3], эта функция принимает
наибольшее значение при х=0,
наименьшее при х=3,
При x=0; y=0
z=(0;0)=0
При x=3;y=0
z=3*0-3-2*0=-3
z(3;0)=-3
[b]при x=3[/b]
z=3y-3-2y=y-3 - как функция одной переменной 0 ≤ y ≤ 3
Эта функция принимает наименьшее при y=0,
наибольшее значение при y=3,
z(3;0)=-3
z(3;3)=0
Из всех найденных выбираем наибольшее и наименьшее.
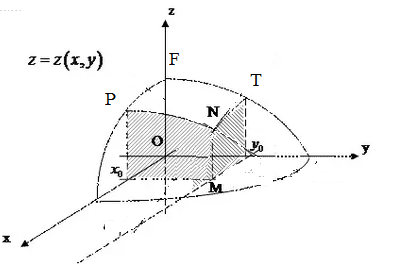
Геометрический смысл задачи на наибольшее и наименьшее значение в области.
На рис. над областью поверхности FPNT.
Точки экстремума нет. ( ни вершины "горы", ни "впадины" )
Поэтому исследуем только на границе.
При пересечении плоскостью x=x_(o) ( в задаче х=3) получили на срезе линию PN. Наибольшее значение в точке P, наименьшее в точке N.
При пересечении плоскостью y=y_(o) ( в задаче х=3) получили на срезе линию NT. Наибольшее значение в точке T, наименьшее в точке N.
На рис. наибольшее в точке F, наименьшее в точке N