Задача 34909 Найти наименьшее и наибольшее...
Условие
функции
z = f (x, y) в замкнутой области D , заданной системой неравенств. Сделать
чертеж.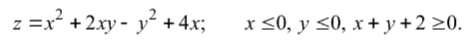
Решение
z`_(y)=2x-2y
Находим стационарные точки:
{z`_(x)=0
{z`_(y)=0
{2x+2y+4=0
{2x-2y=0 ⇒ y=x
2x+2x+4=0
x=-1
y=-1
M(-1;-1) cтационарная точка, принадлежит области.
Находим вторые частные производные
z``_(xx)=(2x+2y+4)`_(x)=2
z``_(xy)=(2x+2y+4)`_(y)=2
z``_(yy)=(2x-2y)`_(y)=-2
A=z``_(xx)(M)=2
B=z``_(yy)(M)=-2
C=z`_`(xy)(M)=2
Δ=AB-C^2=2*(-2)-2^2 < 0
точка M не является точкой экстремума
Исследуем на границе
1) х=0
z=0+2*0*y-y^2+4*0
z=-y^2 - функция одной переменной -2 ≤ у ≤ 0
при у=-2 принимает наименьшее значение z=-4
при у=0 принимает наибольшее значение z=0
2) y=0
z=x^2+4x - функция одной переменной -2 ≤ х ≤ 0
при х=-2 принимает наименьшее значение z=-4
при х=0 принимает наибольшее значение z=0
3) х+у+2=0
y=-x-2
z=x^2+2x*(-x-2)-(-x-2)^2+4*x
z=-2x^2-4x-4- функция одной переменной -2 ≤ х ≤ 0
y`=-4x-4
y`=0
x=-1
при х=-1 принимает наибольшее значение z=-2
Выбираем из всех найденных значений наибольшее и наименьшее
z(0;0)=0 - наибольшее значение в области
z(-2;0)=-4 наименьшее значение в области
Все решения
[youtube=https://youtu.be/va9Ml47FCMI]
[youtube=https://youtu.be/iGGzNJfF8Pg]