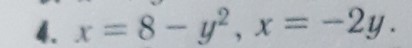Двойные интегралы, вычисление объемов

Построить область интегрирования изменить порядок интегрирования в интеграле

Вычислить двойные интегралы

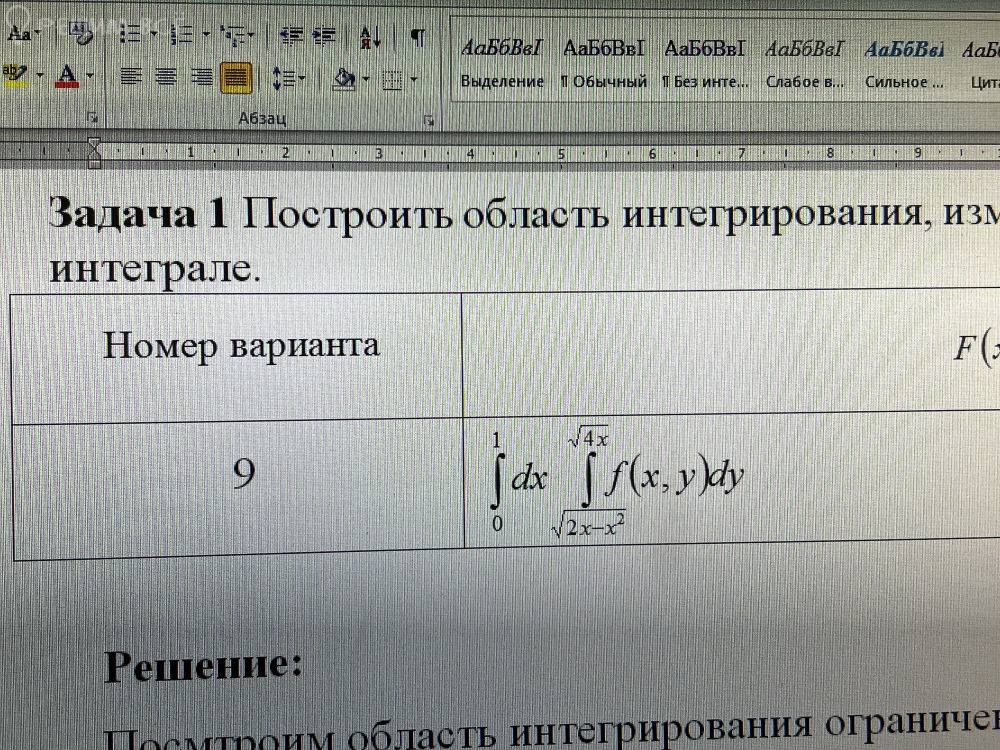
∫∫(8xy + 18x^2y^2) dydx, если D: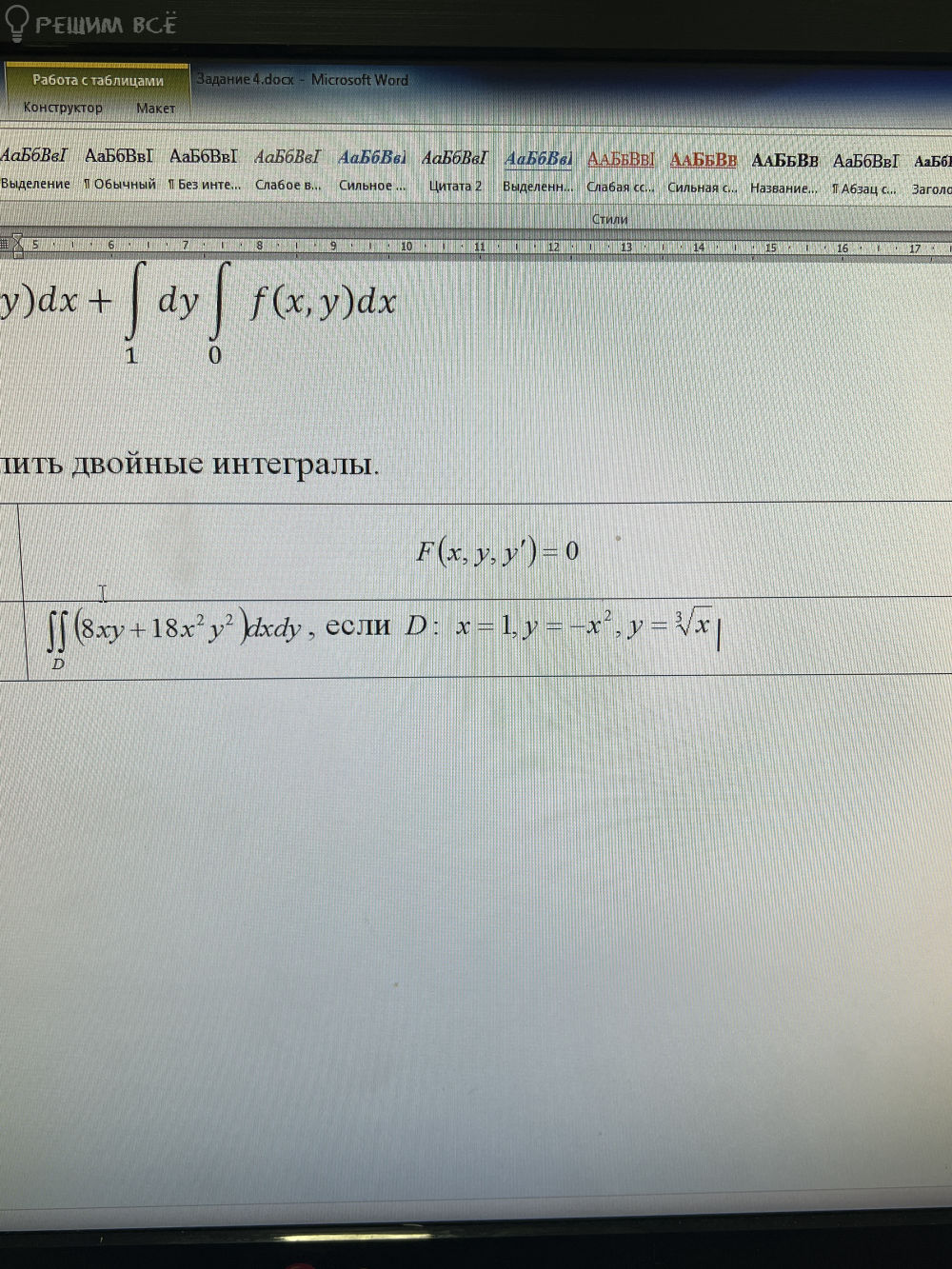

Вычислить двойной интеграл в области D

3. ∬_D e^(2*(x+y)) dx dy

D: {x ∈ [0,1] y ∈ [0,1]}

∭ (2x^3 + 3y + z)dxdydz | V: 2 ≤ x ≤ 3, -1 ≤ y ≤ 2, 0 ≤ z ≤ 4

Вычислить интеграл , где область
D – треугольник с вершинами A(-1;2), B(3;4), C(6;2)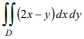

Вычисление повторного интеграла

С помощью двойных интегралов вычислить в полярных координатах площадь плоской фигуры, ограниченной указанными линиям
(x^2+y^2)^3 = 4x^2y^2

Задача 5. Найти объем тела, заданного ограничивающими его поверхностями. 2 2 _ _5 2 — 1.х’ + у” =2у, л —2- х’, # =0.

Задача 3.

Задача 4.вычислить

Изменить порядок интегрирования, пожалуйста полностью и подробно

Вычислить, полностью и подробно
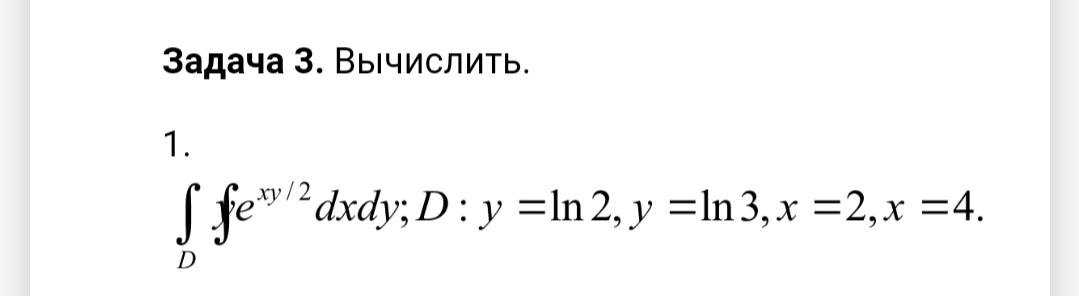
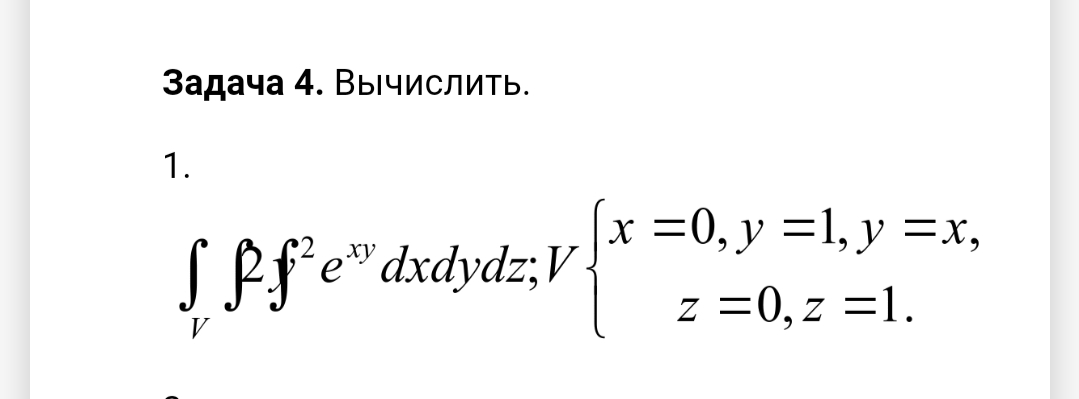
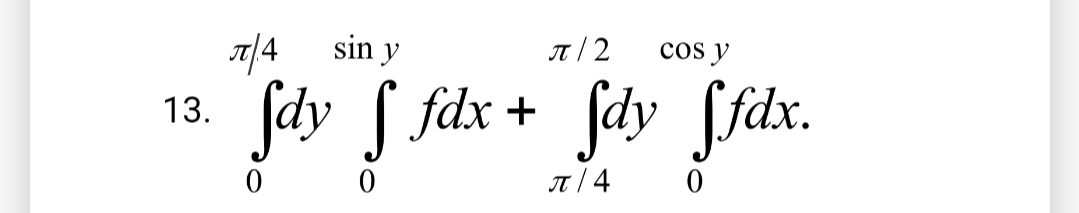
∫∫D y e^(xy/4) dxdy; D : y = ln 2, y = ln 3, x = 4, x = 8.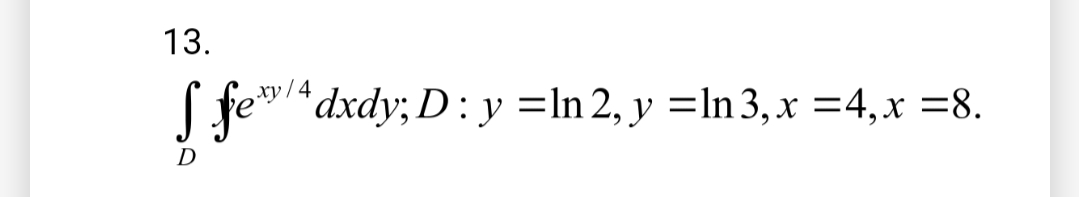

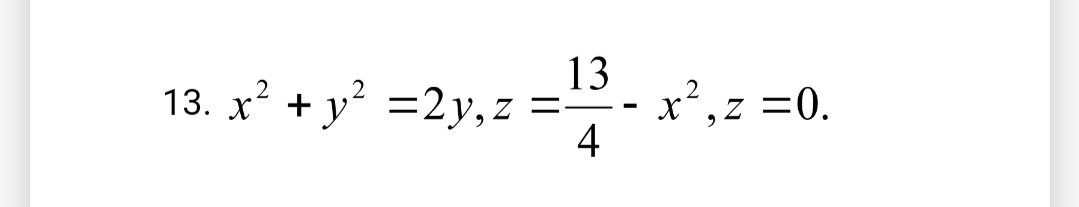
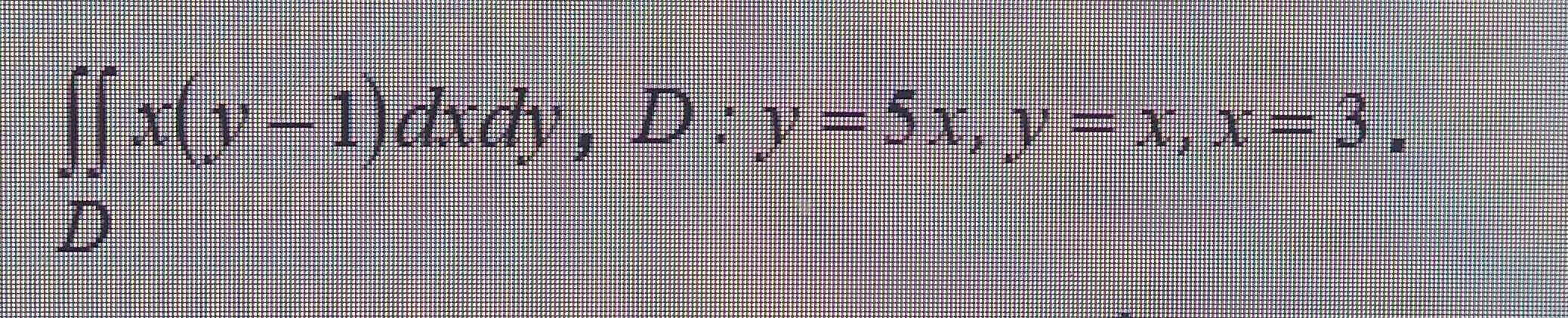
Найти объем тела, заданного ограничивающими его поверхностям, полностью и подробно

Вычислить двойной интеграл по указанной области D. Область интегрирования изобразить на чертеже.

Вычислите двойной интеграл от функции f(x, y) = 2x − 5y + 1
по треугольнику с вершинами A(3; 4), B(3; 6), C(6; 4) .

Добавьте , нарисуйте рисунок к этому заданию , решение не обязательно.

Вычислить интегралы с помощью замены переменных:

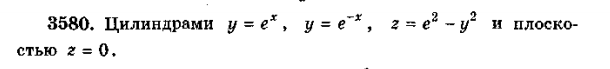
∫∫_(G) xy dx dy, G - область, ограниченная линиями xy=1, x+y=5/2.

Вычислить момент инерции относительно Ox сферической оболочки x^2+y^2+z^2=R^2(x>=0).

Найти объем тела ограниченного конической поверхностью (z-2)^2=x^2/3+y^3/2 и плоскостью z=0.

Изменить порядок интегрирования: ∫[0,1]∫[0,∛y]f dx dy + ∫[1,2]∫[0,2-y]f dx dy

Найти объем тела ограниченного конической поверхностью (z-2)^2=x^2/3+y^3/2 и плоскостью z=0.

Найти объем тела, заданного ограничивающими его поверхностями. При вычислении перейти к полярным координатам
z=1-x^2-y^2
z=0
y=x
y=sqrt(3)*x x⩾0, y⩾0

Найти объем тела, заданного ограничивающими его поверхностями. При вычислении перейти к полярным координатам
z=sqrt(x^2+y^2)
z=0
x2+y2=R^2

Найти объем тела, заданного ограничивающими его поверхностями. При вычислении перейти к полярным координатам
z=x^2+y^2
z=0
x2+y2=R^2

Вычислить тройной интеграл:

∫∫∫_V ( dx / ( (1 + x/1 + y/2 + z/4)^4 ) )

если тело V ограничено поверхностями x = 0, y = 0, z = 0 и x/2 + y/3 + z/4 = 1.

Вычислить с помощью тройного интеграла объём тела, ограниченного указанными поверхностями : z=sqrt(1-y), y=x^2, z=0

Задача 7. Найти площадь фигуры, ограниченной данными линиями.

x^2 - 2x + y^2 = 0, x^2 - 4x + y^2 = 0, y = 0, y = x.

Вычислить двойной интеграл от функции F(x,y)=2x-5y+1 по треугольнику с вершинами A(3,4), B(4,5), C(6,4)

4 задание , решить возможно ?

Здравствуйте. Помогите пожалуйста решить задание.
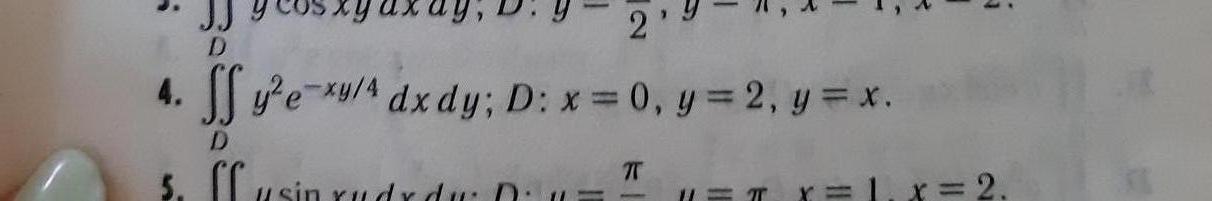
Нарисуйте область, ограниченную заданными поверхностями:

Найти объем данного твердого тела, ограниченный эллиптическим параболоидом z = 4-x^2 - 4y^2, цилиндром x^2 + y^2 = 1 и плоскостью z = 0.

Найдите, пожалуйста, двойной интеграл!!! (Записан справа) Область D задана системой (слева).

9.3.151. Найти объем тела, ограниченного однополосным гиперболоидом x^2 + y^2/4 - z^2 = 1, и плоскостями z = 0, z = 3.

Вычислить объем тела z=x² (параболического цилиндра) ограниченного плоскостями
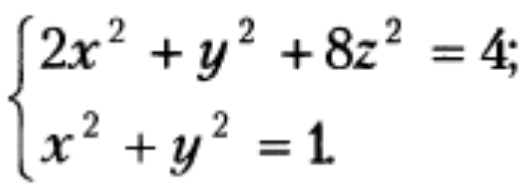
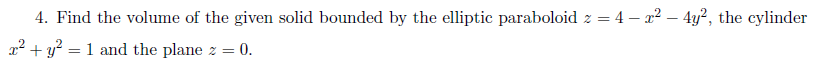
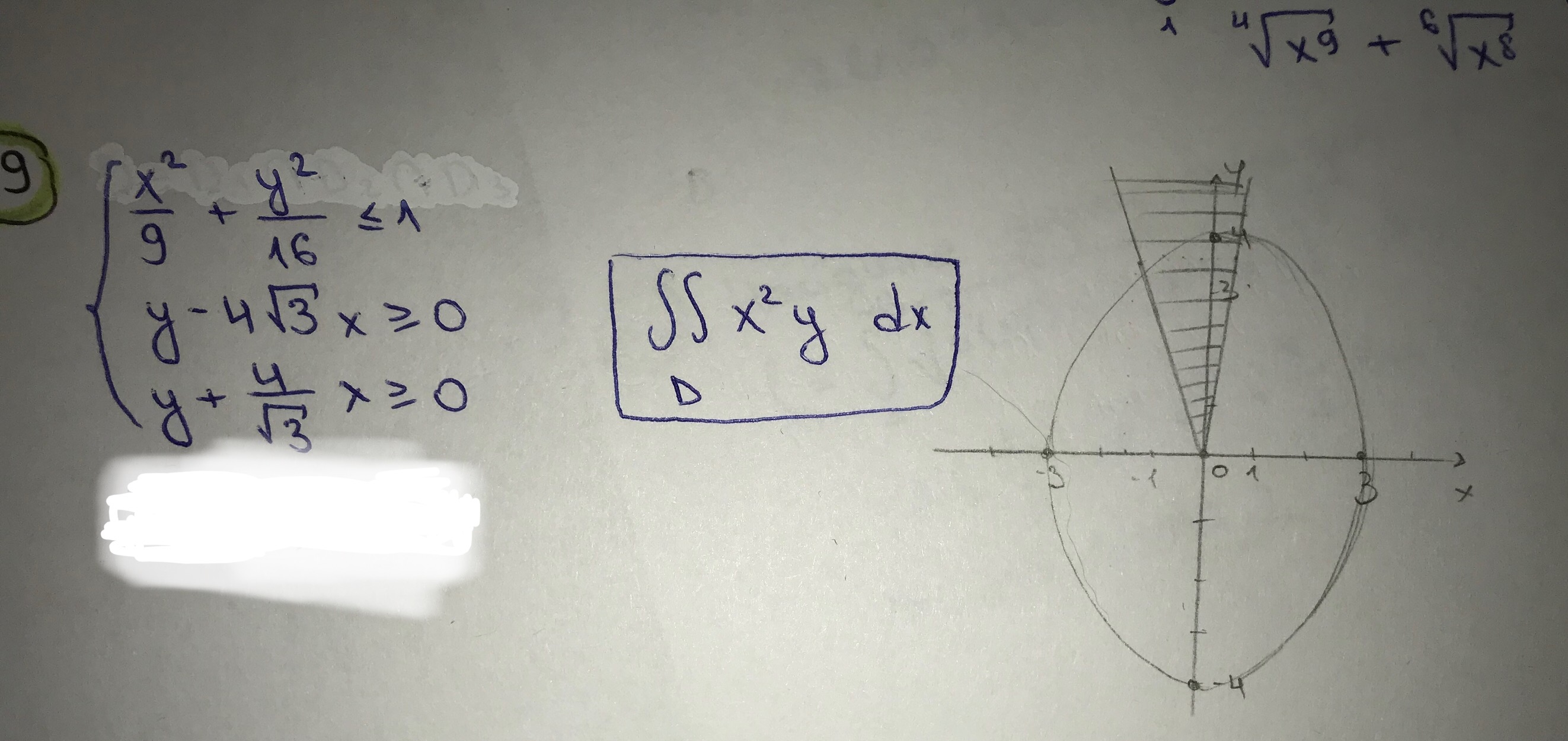
y=0, z=0, x+y=2

Вычислить двойной интеграл (y^2e^-xy/4)dxdy. D:x=0. y=2. y=x

Помогите решить 1-2-3 задание

Вариант 6
1. В интеграле ∫∫_(D)f(x,y)dxdy расставить пределы интегрирования двумя способами, если D: y=√2−x², y=x².
2. Вычислить двойной интеграл ∫∫D(y−x)dxdy по области D, ограниченной указанными линиями: y=x, y=x².
3. Вычислить двойной интеграл ∫−√2√2dx ∫−√2−x²0 (xy/(x²+y²)) dy, используя полярные координаты.

Вычислить объем тела,ограниченного параболоидом z=(x^2/4)+(y^2/2) и плоскостью z=1

Вычислить двойной интеграл (18x^2y^2+32x^3y^3)dxdy. D:x=1. y=x^3. y=-∛x

2. Вычислить двойной интеграл по области D, ограниченной указанными линиями.

2.18. ∫∫ xy^3 dxdy, D: y^2 = 1 - x, x ≥ 0.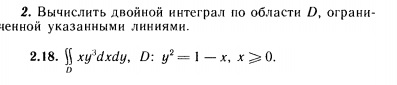

1. Представить двойной интеграл ∫∫ᴰ f(x, y)dxdy в виде повторного интеграла с внешним интегрированием по ...

3. Вычислить двойной интеграл, используя полярные координаты.

3.18. ∫ от 0 до 2 dx ∫ от 0 до √(4-x²) (xy/√(x² + y²)) dy.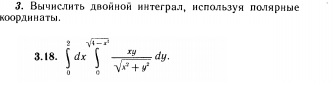

Вариант 4.
1. Изменить порядок интегрирования:
[m]
\int_{0}^{1} \int_{0}^{\sqrt{y}} f(x, y) dx \, dy + \int_{1}^{2} \int_{0}^{\sqrt{2-y}} f(x, y) dx \, dy.
[/m]
2. Перейти в полярные координаты
[m]
\int_{0}^{1} \int_{\sqrt{1-x^2}}^{1} f(x, y) dy \, dx
[/m]
3. Вычислить [m]\iint_{D} 12y \sin 2y \, dx \, dy[/m], где
[m]D: \, x = 3, \, x = 2, \, y = \frac{\pi}{4}, \, y = \frac{\pi}{2}[/m].

4. Вычислить [m]\iiint_{V} (x + y + z) \, dv[/m], где область [m]V[/m] ограничена плоскостями [m]x = 0, \, y = 0, \, z = 0, \, x = 2, \, y = 4, \, z = 5[/m].

5. Вычислить [m]\int_{C} y^2 \, ds[/m], где [m]C[/m] — первая арка циклоиды
[m]
x = a(t - \sin t), \quad y = a(1 - \cos t).
[/m]
6. Вычислить [m]\int_{AB} (x^2 - y^2) \, ds[/m], где [m]AB[/m] — дуга параболы
[m]
y = x^2 \text{ от точки } A(0,0) \text{ до точки } B(2,4).
[/m]

необходимо найти двойной интеграл по области D, ограниченной
указанными линиями.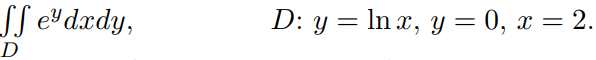

Вычислите двойной интеграл от функции f(x, y) = 2x − 3y + 2
по треугольнику с вершинами A(5; 2), B(5; 4), C(8; 2)

Вычислить ∫(D)∫((4/5)xy+9x^2y^2)dxdy, где D=>x=1, y=√x, y=-x^3

Вычислить двойной интеграл ∫ ∫ 2ydxdy где область D y=sqrt(x), y=0, x+y=2

3. Изменить порядок интегрирования в двукратном интеграле

[m]
\int_0^2 dx \int_{x^2}^{2x} f(x,y)dy
[/m]

4. Перейти к полярным координатам в

[m]
\iint_D f(x,y)dxdy,
[/m]

где D:

[m]
x^2 + y^2 = 1, \quad r = 2 + \cos \varphi
[/m]