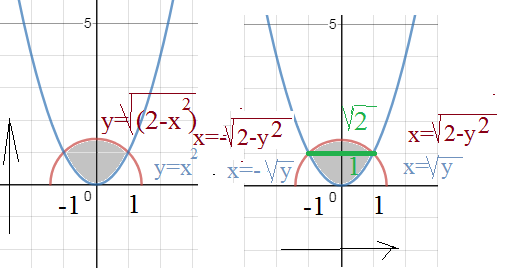Задача 36550 ...

priora844

2019-04-29 11:15:40

Помогите решить 1-2-3 задание

Вариант 6
1. В интеграле ∫∫_(D)f(x,y)dxdy расставить пределы интегрирования двумя способами, если D: y=√2−x², y=x².
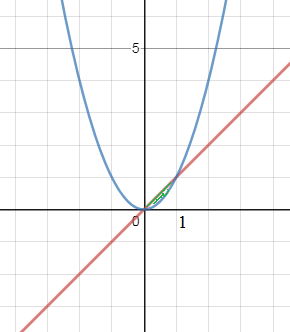
2. Вычислить двойной интеграл ∫∫D(y−x)dxdy по области D, ограниченной указанными линиями: y=x, y=x².
3. Вычислить двойной интеграл ∫−√2√2dx ∫−√2−x²0 (xy/(x²+y²)) dy, используя полярные координаты.

sova

2019-04-29 12:20:47

★

1. см. рис. 1

1 вертикальная область
= ∫ ^(1)_(-1)dx ∫ ^(sqrt(2-x^2))_(x^2)f(x;y)dy


2 горизонтальная область
= ∫ ^(0)_(1)dy ∫ ^(sqrt(y))_(-sqrt(y))f(x;y)dx+
+ ∫^(sqrt(2)_(1)dy ∫ ^(sqrt(2-y^2)_(-sqrt(2-y^2)f(x;y)dx

2. cм рис.2
∫ ∫ _(D)(y-x)dxdy= ∫ ^(1)_(0)dx ∫ ^(x)_(x^2)(x-y)dy=

= ∫ ^(1)_(0) (xy-(y^2/2))|^(x)_(x^2)dx=

=∫ ^(1)_(0) [b]([/b] x^2-(x^2/2) - (x^3-(x^4/2)) [b])[/b]dx=

=∫ ^(1)_(0) [b]([/b] (x^2/2) - x^3+(x^4/2) [b])[/b]dx=

=(x^3/6)^(1)_(0) - (x^4/4)|^(1)_(0) + (x^5/10)^(1)_(0)=

=(1/6)-(1/4)+(1/10)=