Задача 59992 Задача 4.вычислить...
Условие
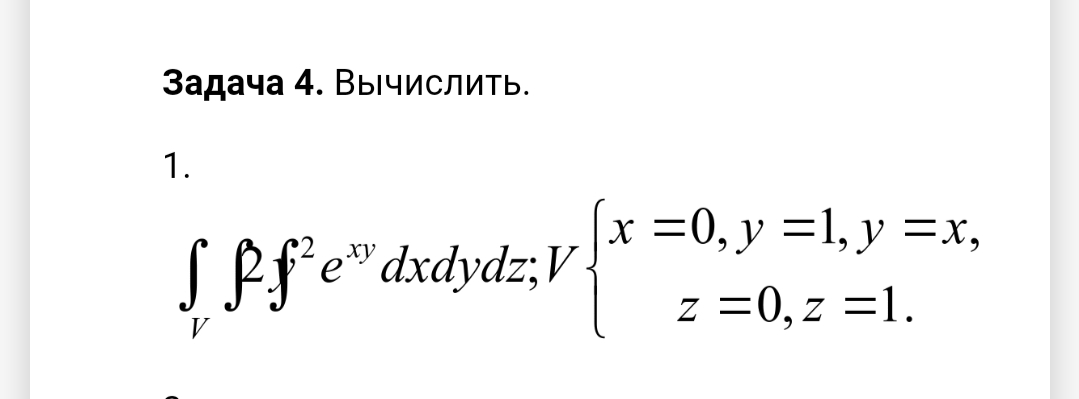
нет в списке ВУЗ
636
Решение
★
0 ≤ y ≤ 1
0 ≤ x ≤ y
0 ≤z ≤ 1
∫∫∫_(V) 2y^2e^(xy)dxdydz= ∫∫ _(D) 2y^2e^(xy)([blue] ∫_(0)^(1)dz[/blue]) dxdy=
=∫∫ _(D) 2y^2e^(xy)([blue] (z)|_(0)^(1)[/blue]) dxdy=
=∫∫ _(D) 2y^2e^(xy)dxdy[red][b]=[/b][/red]
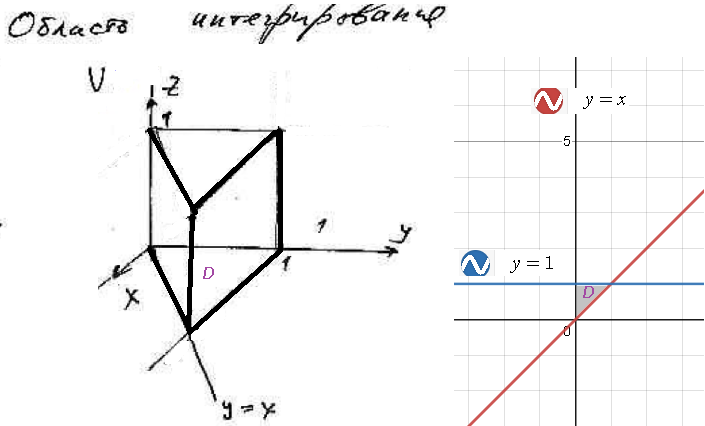
Область интегрирования двойного интеграла D: ( см рис.2)
0 ≤ y ≤ 1
0 ≤ x ≤ y
[red][b]=[/b][/red] ∫_(0) ^(1)(2y^2[blue] ∫_(0)^(y) e^(xy)dx[/blue])dy=
= ∫ _(0) ^(1)(2y^2*(1/y)[blue] ∫^(y)_(0)e^(xy) d(xy) [/blue])dy=
=∫ _(0) ^(1)(2y^2*(1/y)[blue] (e^(xy))| ^(1)_(0)) [/blue])dy=
=∫ _(0) ^(1)(2y^2*(1/y)[blue] (e^(y*y)-e^(0*y)) [/blue])dy=
=∫ _(0) ^(1)(2y*(e^)y^(y^2)-1)dy=
=(e^(y^2)-y)|_(0) ^(1)=e-1-(e^(0)-0)=[red][b]e-2[/b][/red]