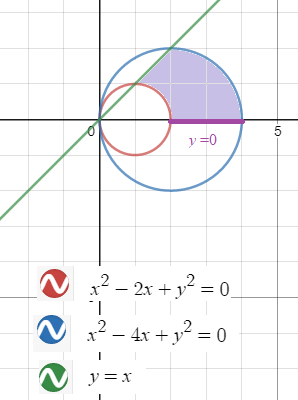Задача 55280 ...
Условие
математика ВУЗ
480
Решение
★
Полярные координаты:
[m]x= ρ cos φ [/m]
[m]y= ρ sin φ [/m]
[m]x^2+y^2= ρ ^2[/m]
dxdy= ρ d ρ d φ
[m]x^2-2x+y^2= 0 ⇒ ρ ^2-2ρ cos φ=0 ⇒ ρ =2cos φ [/m]
[m]x^2-4x+y^2=0 ⇒ ρ ^2-4ρ cos φ=0 ⇒ ρ =4cos φ [/m]
Область D:
[m]0 ≤ φ ≤ \frac{π}{4}[/m]
[m]2cos φ ≤ ρ ≤ 4cos φ [/m]
[m]= ∫^{\frac{π}{4}}_{0}( ∫ ^{ 4cos φ}_{ 2cos φ} ρ d ρ )d φ =∫^{\frac{π}{4}}_{0}(\frac{ ρ^2}{2})|^{ 4cos φ}_{ 2cos φ}d φ=∫^{\frac{π}{4}}_{0}6cos^2 φ d φ =3∫^{\frac{π}{4}}_{0}(1+cos2 φ)d φ =(3 φ +\frac{3}{2}sin2 φ) | ^{\frac{π}{4}}_{0}=[/m]
[m]=3 \frac{π}{4}+\frac{3}{2}sin(2 \cdot \frac{π}{4})=\frac{3π}{4}+\frac{3}{2}[/m]