Задача 59991 Задача 3. ...
Условие
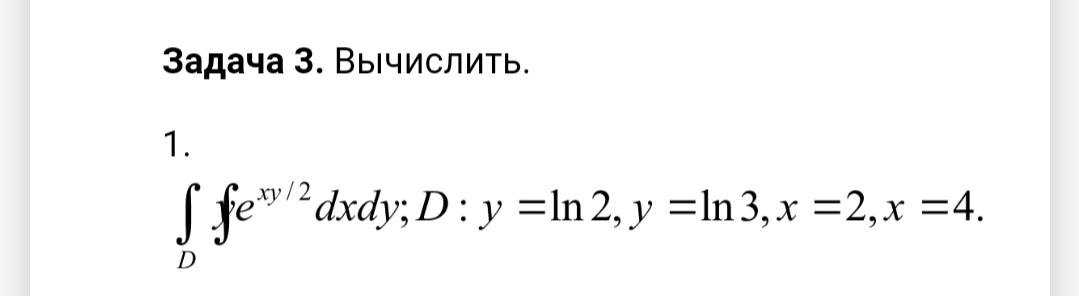
Решение
2 ≤ x ≤ 4
ln2 ≤ y ≤ ln3
[m]∫∫_{D} =∫_{ln2} ^{ln3}y( ∫ ^{4}_{2}e^{\frac{xy}{2}}dx)dy=[/m]
так как[m] (\frac{xy}{2})`_{x}=\frac{y}{2}dx[/m] ⇒
[m] =∫_{ln2} ^{ln3}y\cdot \frac{2}{y} ( ∫ ^{4}_{2}e^{\frac{xy}{2}}\cdot \frac{y}{2}dx)dy=[/m]
[m] =∫_{ln2} ^{ln3} 2 ( e^{\frac{xy}{2}})|^{x=4}_{x=2}dy=[/m]
[m] =∫_{ln2} ^{ln3} 2 ( e^{\frac{4y}{2}}-e^{\frac{2y}{2}})dy=[/m]
[m] =∫_{ln2} ^{ln3} 2 ( e^{2y}-e^{y})dy=[/m]
[m] =∫_{ln2} ^{ln3} e^{2y}d(2y)-2∫_{ln2} ^{ln3} e^{y}dy=[/m]
[m]=(e^{2y}-2e^{y})|_{ln2} ^{ln3} =[/m]
[m]=e^{2ln3}-e^{2ln2}-2e^{ln3}+2e^{ln2}=[/m]
[m]=e^{ln3^2}-e^{ln2^2}-2e^{ln3}+2e^{ln2}=[/m]
применяем основное логарифмическое тождество
=3^2-4^2-2*3+2*2=... считаем