Задача 33696 ...

ermakhan001

18 февраля 2019 г. в 19:16

Вычислить двойной интеграл (18x²y²+32x³y³)dxdy. D:x=1. y=x³. y=–∛x

sova

18 февраля 2019 г. в 19:33

★

∫ ∫ _D (18x2y2+32x3y3)dxdy=

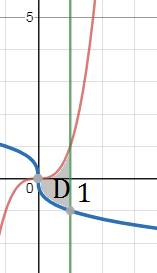
= ∫ ¹₀( ∫ ^x3_–∛x( 18x²y²+32x³y³)dy=

=∫ ¹₀(18x²·(y³/3) + 32x³·(y⁴/4))|^y=x3_y=–∛x dx=

=∫ ¹₀(6x²·((x³)³–(–∛x)³) +8x³·(x³⁴ – (– ∛x)⁴)dx=

=∫ ¹₀(6x²·(x⁹+x) +8x³·(x¹² – ∛(x⁴))dx=

=∫ ¹₀(6x¹¹+6x³+8x¹⁵ – 8x^13/3)dx=

=(6·(x¹²/12) +6·(x⁴/4)+8·(x^16/16 –8·(x^16/3/(16/3))|¹₀=

=2·1+(3/2)·1+(1/2)·1–(3/2)·1=5/2