Задача 58025 ...

6028ed4d3cfdeb46290c8b33

21 февраля 2021 г. в 09:54

Вычислить интегралы с помощью замены переменных:

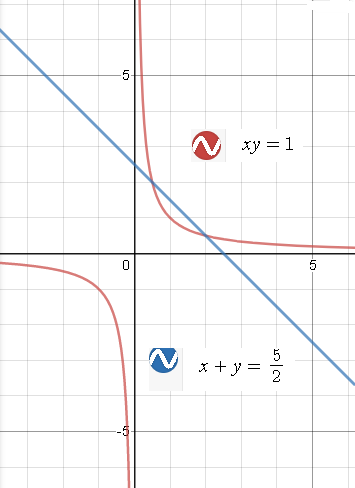
∫∫_G xy dx dy, G – область, ограниченная линиями xy=1, x+y=5/2.

5f3ea7e3faf909182968ddd9

21 февраля 2021 г. в 10:34

★

∫∫_G xydxdy= ∫ ²_0,5 (∫^2,5–x_1/x xydy)dx= ∫ ²_0,5x· (∫^2,5–x_1/x ydy)dx=


=∫ ²_0,5x· (y²/2))|^2,5–x_1/x)dx=

=∫ ²_0,5x· ((2,5–x)²/2)–(1/x)²/2)dx=

=∫ ²_0,5x·(1/2)·(6,25–5x+x²–(1/x²))dx=

=(1/2)∫ ²_0,5(6,25x–5x²+x³–(1/x))dx=

=(1/2)·(6,25·(x²/2)–5·(x³/3)+(x⁴/4)–ln|x|)|²_0,5=


=(1/2)·(6,25·(2²/2)–5·(2³/3)+(2⁴/4)–ln|2|)– (1/2)·(6,25·(0,5²/2)–5·(0,5³/3)+(0,5⁴/4)–ln|0,5|)=

=6,25–(20/3)+2–(1/2)ln2–(1/16)·6,25+(5/48)–(1/128)+(1/2)ln(1/2)=...



ln(1/2)=–ln2