Задача 45247 Вычислите двойной интеграл от функции...

polinanevolina

2020-03-23 13:32:09

Вычислите двойной интеграл от функции f(x, y) = 2x − 3y + 2
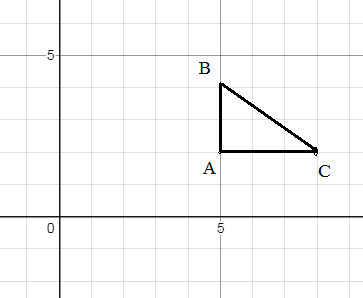
по треугольнику с вершинами A(5; 2), B(5; 4), C(8; 2)

sova

2020-03-23 14:35:50

★

Написать уравнения стороны BC треугольника, как прямой проходящей через две точки

y=kx+b
4=5k+b
2=8k+b
3k=-2
k=-2/3
b=22/3

область D:
5 ≤ х ≤ 8
2 ≤ y ≤ (-2/3)x+(22/3)

∫ ∫ _(D)(2x-3y+2)dxdy= ∫ ^(8)_(5)[b]([/b] ∫ ^((-2/3)x+(22/3))_(0)(2x-3y+2)dy)[b])[/b]dx=

Считаем внутренний интеграл, потом внешний

= ∫ ^(8)_(5) [b]([/b](2xy-(3y^2/2)+2y)|^(y=(-2/3)x+(22/3))_(y=0)[b])[/b]dx=

= ∫ ^(8)_(5)[b]([/b]2x*((-2/3)x+(22/3))-(3/2)*((-2/3)x+(22/3))^2+2*((-2/3)x+(22/3))[b])[/b]dx=


=∫ ^(8)_(5) ( (-4/3)x^2+(44/3)x-(3/2)*((4/9)x^2-(88/9)x+(484/9))-(4/3)x+(44/3)[b])[/b]dx=

=∫ ^(8)_(5) ((-4/3)x^2+(44/3)x-(2/3)x^2+(44/3)x-(242/3)-(4/3)x+(44/3))dx=

=∫ ^(8)_(5) (-2x^2+(84/3)x-(192/3))dx=(-2x^3/3)+28(x^2/2)-64x)|^(8)_(5)=

=(-2/3)*(8^3-5^3)+14*(8^2-5^2)-64*(8-5)=... считайте