Задача 47112 3. Изменить порядок интегрирования в...

boris98

2020-04-14 21:01:24

3. Изменить порядок интегрирования в двукратном интеграле

[m]
\int_0^2 dx \int_{x^2}^{2x} f(x,y)dy
[/m]

4. Перейти к полярным координатам в

[m]
\iint_D f(x,y)dxdy,
[/m]

где D:

[m]
x^2 + y^2 = 1, \quad r = 2 + \cos \varphi
[/m]

sova

2020-04-14 21:40:22

★

1)
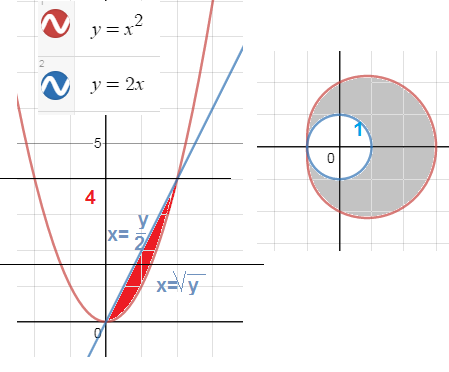
Рассматриваем область как область горизонтального вида
y в полосе от 0 до 4

Уравнения переписываем в виде x= ..; x=..

Cм на рис..

= ∫ ^(4)_(0)dy ∫ ^(sqrt(y))_(y/2)f(x;y)dx

2)
x^2+y^2=1 ⇒ r^2cos^2 φ +r^2sin^2 φ =1 ⇒ r^2=1 ⇒ r=1
Линия входа в область

Линия выхода красная кардиоида r=2+cos φ
∫ ^(2π)_(0)d φ ∫ ^(2+cos φ )_(1)f(rcos φ ; rsin φ )rdr