Задача 49449 Найдите, пожалуйста, двойной интеграл!!!...
Условие
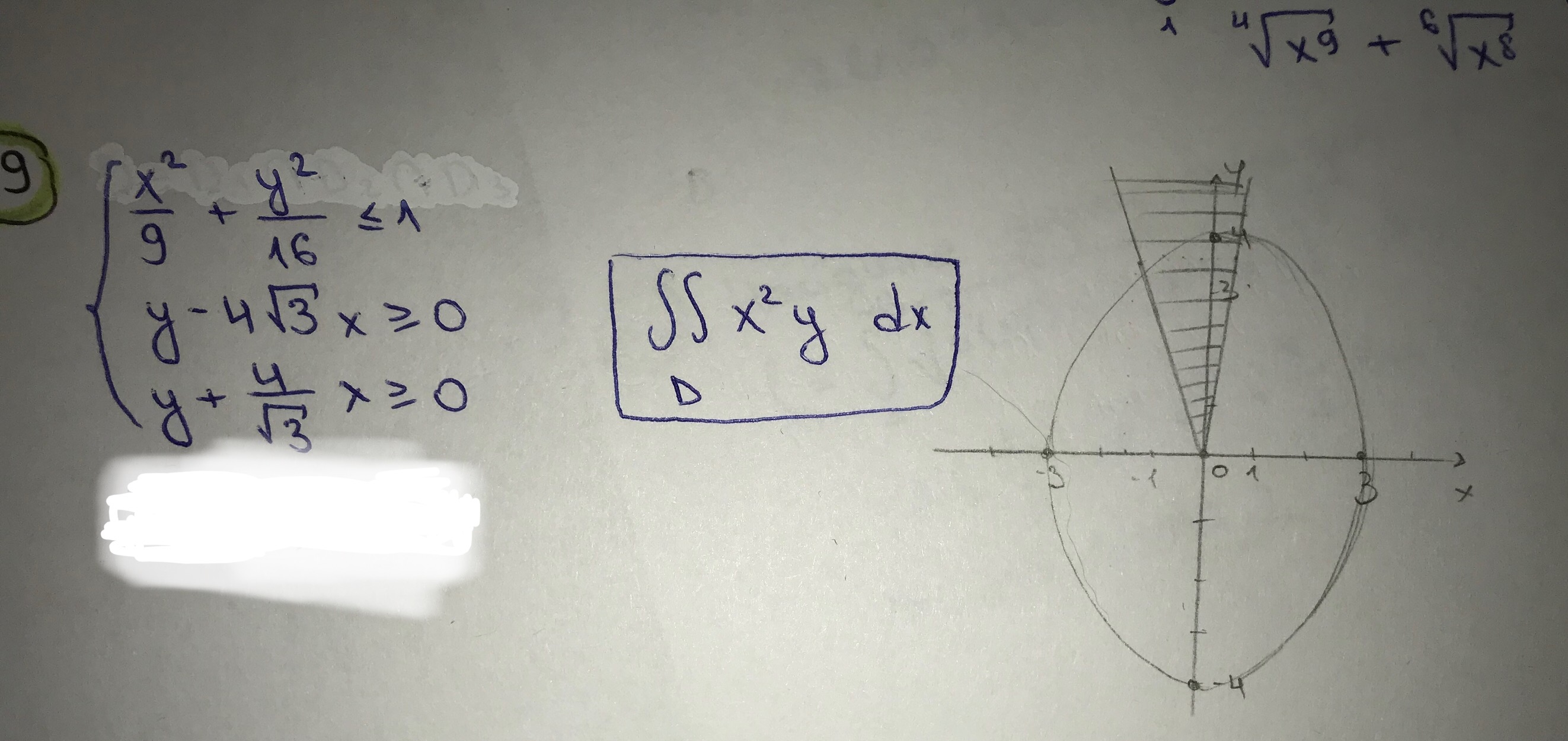
Решение
x=3*r*cos φ
y=4*r*sin φ ⇒ (x^2/9)+(y^2/16)=1 ⇒ r^2=1 ⇒ r=1
Якобиан
abr=[red]3*4*r[/red]
y=4sqrt(3)*x
4*r*sin φ =4*sqrt(3)*3*r*cos φ ⇒ tg φ =3sqrt(3) ⇒ φ =arctg 3sqrt(3)
y=-4x/sqrt(3)
4*r*sin φ =-4*3*r*cos φ/sqrt(3) ⇒ tg φ =-sqrt(3) ⇒ φ =2π/3
= ∫^(1)_(0) dr ∫ ^(2π/3)_(arctg3sqrt(3))(3*r*cos φ )^2*(4*r*sin φ )^2* ([red]12 r[/red])d φ =
=3^2*4^2*12 ∫^(1)_(0)r^5 dr ∫ ^(2π/3)_(arctg3sqrt(3))((1+cos 2φ )/2)*((1-cos2φ)/2 ) d φ =
=432∫^(1)_(0)r^5 dr ∫ ^(2π/3)_(arctg3sqrt(3))(1-cos^2 2φ )d φ =
=432∫^(1)_(0)r^5 dr ∫ ^(2π/3)_(arctg3sqrt(3))(sin^2 2φ )d φ =
=432∫^(1)_(0)r^5 dr ∫ ^(2π/3)_(arctg3sqrt(3))((1-cos4φ )/2)d φ =
=216*(r^6/6)|^(1)_(0) ( φ -(1/4)sin4 φ )| ^(2π/3)_(arctg3sqrt(3)) =...