Задача 51964 Найти объем данного твердого тела,...
Условие
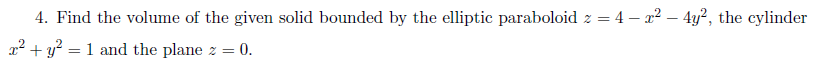
Решение
D: x^2+y^2=1
Переходим к полярным координатам:
x= ρ cos φ
y= ρ sin φ
dxdy=[blue] ρ d ρ d φ
[/blue]
4-x^2-4y^2=[b]4- ρ^2cos^2φ -4 ρsin^2φ [/b]
0 ≤ ρ ≤ 1
0 ≤ φ ≤ 2π
V= ∫^(2π)_(0) ∫ ^(1)_(0) ( [b]4- ρ^2cos^2φ -4 ρ^2sin^2φ [/b]) [blue]ρ d ρ d φ[/blue]=
= ∫^(2π)_(0) (∫ ^(1)_(0) (4 ρ - ρ ^3 cos^2φ -4 ρ^3sin^2φ )d ρ )d φ =
=∫^(2π)_(0)(4( ρ ^2/2)-( ρ ^4/4) cos^2φ-4( ρ ^4/4)sin^2 φ )|^( ρ =1)_( ρ =0)d φ =
=∫^(2π)_(0)(2-(1/4)cos^2φ-sin^2 φ )d φ =
=2 φ|^(2π)_(0) -(1/4) ∫^(2π)_(0) (1+cos2 φ )d φ /2 - ∫ ^(2π)_(0)(1-cos2 φ )/2d φ =
=4π-(1/8)( φ +(1/2)sin2 φ)^(2π)_(0)-((1/2) φ -(1/4)sin2 φ )|^(2π)_(0)=
=4π-(π/4)-π=[b]11π/4 [/b]