Задача 61184 Вычислить интеграл , где область D –...
Условие
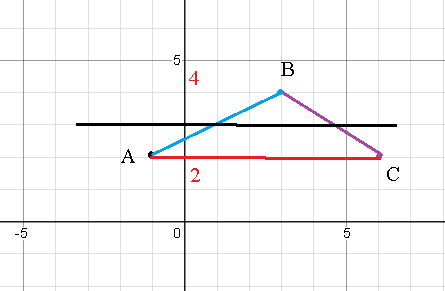
D – треугольник с вершинами A(-1;2), B(3;4), C(6;2)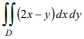
1661
Решение
★
2 ≤ y ≤ 4
Составляем уравнение прямой АВ как прямой, проходящей через две точки
y=(1/2)x+(5/2)
⇒
x=2y-5 - уравнение линии входа в область
Составляем уравнение прямой ВC как прямой, проходящей через две точки
3y+2x=18
⇒
x=(-3/2)y+6 - уравнение линии выхода
Тогда
2y-5 ≤ x ≤ (-3/2)y+6
∫∫_(D)(2x-y)dxdy= ∫ ^(4)_(2) ([b]∫^(2y-5)_((-3/2)y+6) (2x-y)dx[/b])dy=
=∫ ^(4)_(2) ([b](x^2-y*x)|^(2y-5)_((-3/2)y+6) [/b])dy=
=∫ ^(4)_(2) ([b]((2y-5)^2-y*(2y-5)-((-3/2)y+6)^2-y*( (-3/2)y+6))dy=[/b])dy