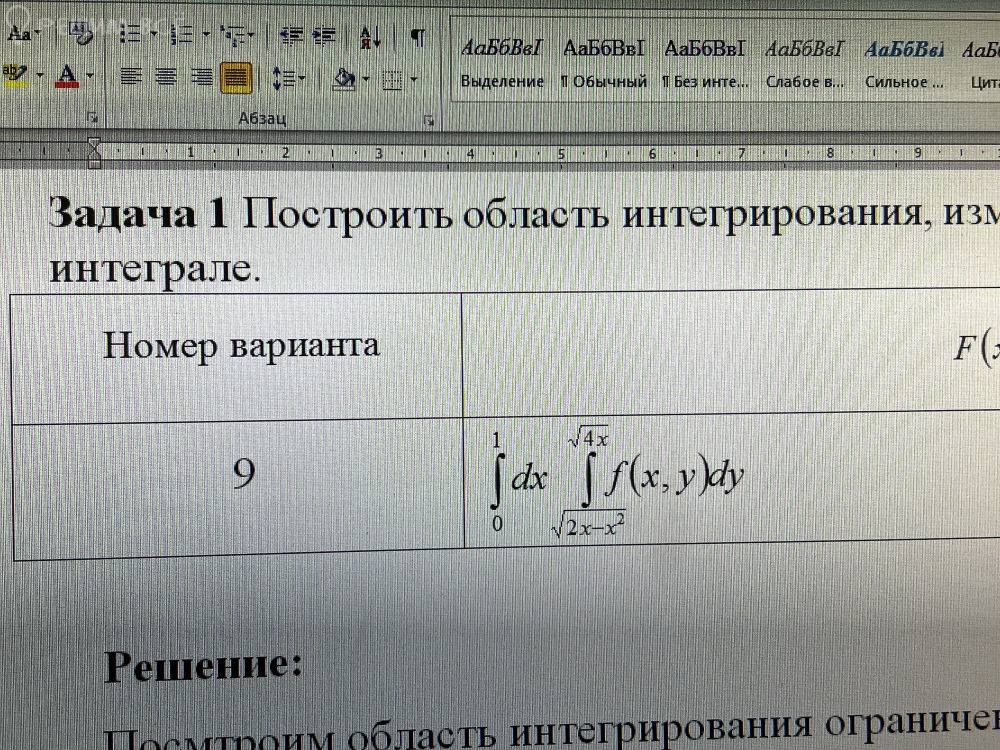
Задача 65496 Построить область интегрирования...
Условие
Решение
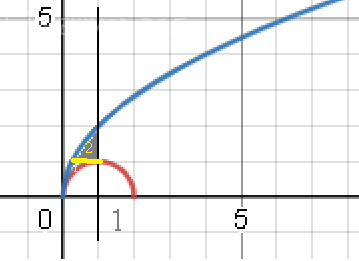
sqrt(2x-x^2) ≤ y ≤ \sqrt{4x}
Строим y=sqrt(2x-x^2) - это полуокружность с центром в точке (1;0) радиуса 1
Возводим в квадрат:
y^2=2x-x^2
x^2-2x+y^2=0
x^2-2x+[red]1[/red]+y^2=[red]1[/red]
[b](x-1)^2+y^2=1[/b] это окружность
[blue]y=sqrt(4x)[/blue] - парабола
y^2=4x ⇒
[blue]x=(1/4) y^2[/blue]
На рисунке область закрашена.
Это область вертикального входа.
Входим в направлении оси Оу
Теперь надо входить в направлении оси Ох
Для этого область делим на две части ( желтая линия y=1)
Тогда
(x-1)^2+y^2=1 ⇒ x-1= ± sqrt(1-y^2) ⇒
левая
x=1-sqrt(1-y^2)
правая
х=1+sqrt(1-y^2)
Области принадлежит левая полуокружность
0 ≤ y ≤ 1
0 ≤ x ≤ 1-sqrt(1-y^2)
Вторая часть
1 ≤ y ≤ 2
(1/4)y^2 ≤ x ≤ 1
x=(1/4)x^2 - левая линия, линия входа в область
x=1 - правая линия, линия выхода из области
Это означает, что интеграл можно представить как сумму интегралов по области 1 и по области 2:
= ∫ _(0)^(1)( ∫ _(0)^(1-sqrt(1-y^2)) f(x;y)dx)dy+ ∫ _(1)^(2)( ∫ _((1/4)y^2)^(1) f(x;y)dx)dy