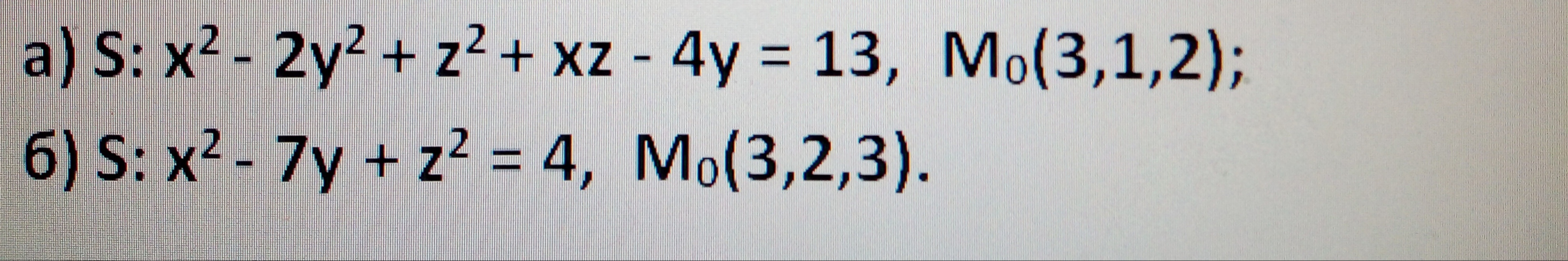Уравнения касательной пл и нормали

Написать уравнение касательной плоскости к сфере: x² + y² + z² = 49 в точке М (2; – 6; 3).

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке M0 (x0,у0,z0). Поверхность, заданную в пункте б): изобразить на чертеже.

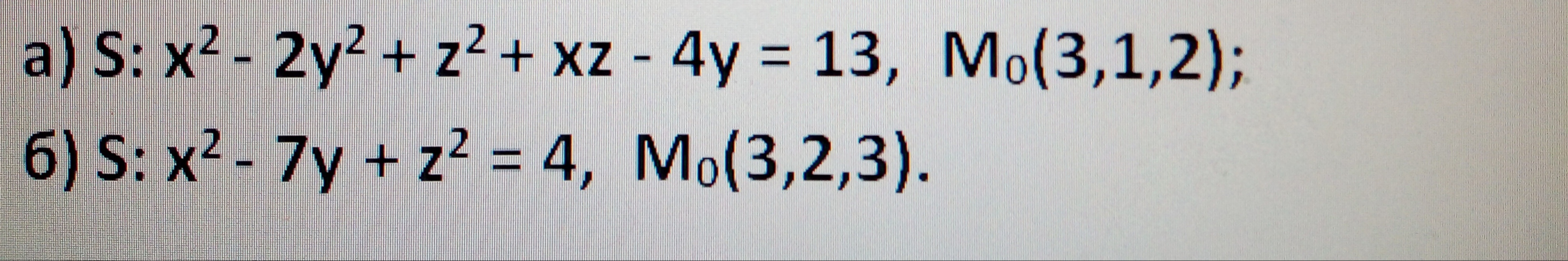
Определить вид поверхности и построить ее в каждой из следующих случаев:
А) х²+2у²––4y–2z=0
B)z²+y²–2z=0

Найти уравнения касательной и нормали к кривой
4x³ – 3xy² + 6x² – 5xy – 8y² + 9x + 14 = 0 в точке M(–2, 3).

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке Mo (хо: уо, zo). Поверхность, заданную в пункте б): изобразить на чертеже.

Написать уравнения касательной плоскости и нормали к поверхностям, заданным уравнениями вида а) z = f(x,y); б) F(x, y, z) = 0 в заданной точке M₀.

а) z = 3x² – y², M₀(1; 1; 2);
б) [m]\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1[/m], M₀([m]\frac{a\sqrt{3}}{3}[/m] ; [m]\frac{b\sqrt{3}}{3}[/m] ; [m]\frac{c\sqrt{3}}{3}[/m]).