Задача 39400 ...
Условие
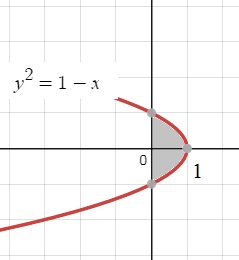
2.18. ∫∫ xy^3 dxdy, D: y^2 = 1 - x, x ≥ 0.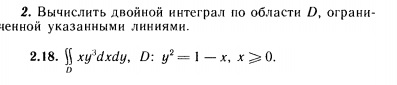
предмет не задан
896
Все решения
-sqrt(1-x) ≤ y ≤ sqrt(1-x)
∫∫ _(D)xy^3dxdy= ∫ ^(1)_(0)xdx ∫^(sqrt(1-x)_(-sqrt(1-x))y^3dy=
= ∫ ^(1)_(0)x [m]\frac{y^4}{4}|^{\sqrt{1-x}}_{-\sqrt{1-x}}[/m]dx=
= ∫ ^(1)_(0)x*[m]\frac{(1-x)^2-(1-x)^2}{4}[/m]dx= ∫ ^(1)_(0)x*[red]0[/red]dx=0