Задача 45989 d^2u/dx^2+d^2u/dy^2+d^2u/dz^2=0,u=1/sqrt(x^2+y^2+z^2) ...
Условие
Данное уравнение данной функции u должно быть выполнено.
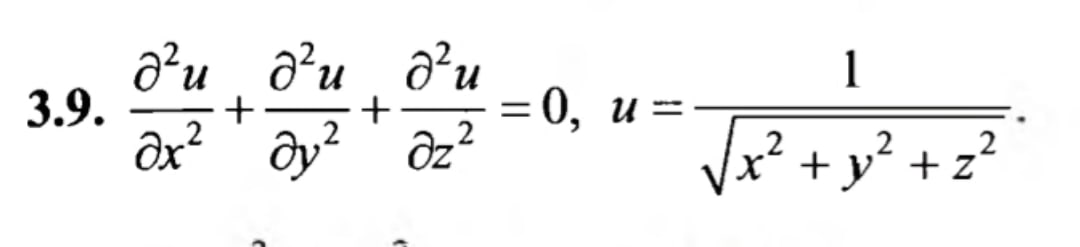
Решение
[m]=(x^2+y^2+z^2)^{-\frac{1}{2})`_{x}}=[/m]
[m]=-\frac{1}{2}\cdot (x^2+y^2+z^2)^{-\frac{1}{2}-1}\cdot (x^2+y^2+z^2)`_{x}=-x\cdot (x^2+y^2+z^2)^{-\frac{3}{2}}[/m]
∂ u/ ∂ y=[m](\frac{1}{\sqrt{x^2+y^2+z^2}})`_{y}=[/m]
[m]=(x^2+y^2+z^2)^{-\frac{1}{2})`_{y}}=[/m]
[m]=-\frac{1}{2}\cdot (x^2+y^2+z^2)^{-\frac{1}{2}-1}\cdot (x^2+y^2+z^2)`_{y}=-y\cdot (x^2+y^2+z^2)^{-\frac{3}{2}}[/m]
∂ u/ ∂z=[m](\frac{1}{\sqrt{x^2+y^2+z^2}})`_{z}=[/m]
[m]=(x^2+y^2+z^2)^{-\frac{1}{2})`_{z}}=[/m]
[m]=-\frac{1}{2}\cdot (x^2+y^2+z^2)^{-\frac{1}{2}-1}\cdot (x^2+y^2+z^2)`_{z}=-z \cdot (x^2+y^2+z^2)^{-\frac{3}{2}}[/m]
∂^2 u/ ∂ x^2=[m](-x\cdot (x^2+y^2+z^2)^{-\frac{3}{2}})`_{x}=[/m]
[m]=-(x^2+y^2+z^2)^{-\frac{3}{2}}+\frac{3}{2} x\cdot (x^2+y^2+z^2)^{-\frac{5}{2}}\cdot (2x)[/m]
∂^2 u/ ∂ y^2=[m](-y\cdot (x^2+y^2+z^2)^{-\frac{3}{2}})`_{y}[/m]
[m]=-(x^2+y^2+z^2)^{-\frac{3}{2}}+\frac{3}{2} y\cdot (x^2+y^2+z^2)^{-\frac{5}{2}}\cdot (2y)[/m]
∂^2 u/ ∂ z^2=[m](-z\cdot (x^2+y^2+z^2)^{-\frac{3}{2}})`_{z}[/m]
[m]=-(x^2+y^2+z^2)^{-\frac{3}{2}}+\frac{3}{2} z\cdot (x^2+y^2+z^2)^{-\frac{5}{2}}\cdot (2z)[/m]
∂^2 u/ ∂ x^2+ ∂^2 u/ ∂ y^2+ ∂^2 u/ ∂ x^2=
[m]=-3(x^2+y^2+z^2)^{-\frac{3}{2}}+3\cdot (x^2+y^2+z^2)^{-\frac{3}{2}}=0[/m]- верно
