Многочлены

x⁴+2x³+5x²+4x–12=0

Пример 3. Найдите член разложения, содержащий у⁷.

Найдите значение многочлена Р(х) в точке х = а:
4) P(x) = – 3x⁶+ 22³ – 4x² –2x + 10, a = –1.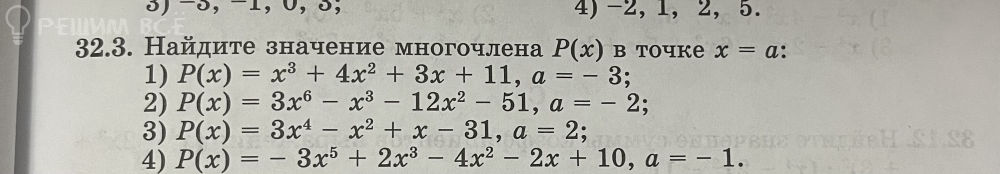

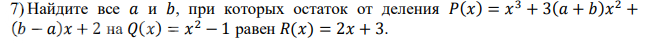
7) Найдите все а и b, при которых остаток от деления ….

Остаток от деления многочлена Р(х) на линейный двучлен 2х — 3 равен 5, а от деления на линейный двучлен х + 6 равен 3. Найдите остаток от деления многочлена: Р(x) на квадратный трехчлен 2х² + 9х — 18.

4 и 5 номер пж с решением а не только ответ

Найдите многочлен Р(х), если известно, что
Р(х)+р(х–1)≡4х²+2х–3

При каких значениях a и p равны мночлены P(x) и K(x).
p(x)=x3–3x2+2x–5 k(x)=ax3+(a+p)x2+2x–5

Найти коэффициент при x^k в разложении данного выражения P по полиномиальной фор–
муле, полученный после раскрытия скобок и приведения подобных членов.

Найти наибольший член разложения бинома (a + b)^n, где a = √5, b = 2,3, n = 17.

сколько членов разложения бинома являются целыми числами. На фото сам бином

Найти числовой коэффициент в члене разложения (1/2+x⁸)⁸⁰⁰,содержащем x⁶³⁸⁴

Найдите действительные корни многочлена h(x)=x³–x²–8x+12 и разложить множители

х⁴ – 2х³ – 2х² – 2х + 1 = 0 уравнение

6x⁴ – 18x³ – 27x² + 40x – 12 = 0.

Найдите полином Лагранжа, который интерполирует точки (2, 4), (3, 1), (5, 7), и нарисуйте его график.

при каких значениях a многочлены p(x) и k(x) равны p(x)= (2–a²)x³+3x²+2x–9, k(x)= ax³+(a²+2a)x²+2x–9

P(x)=x³–2x²–2x+a²–3a
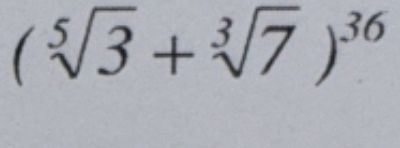
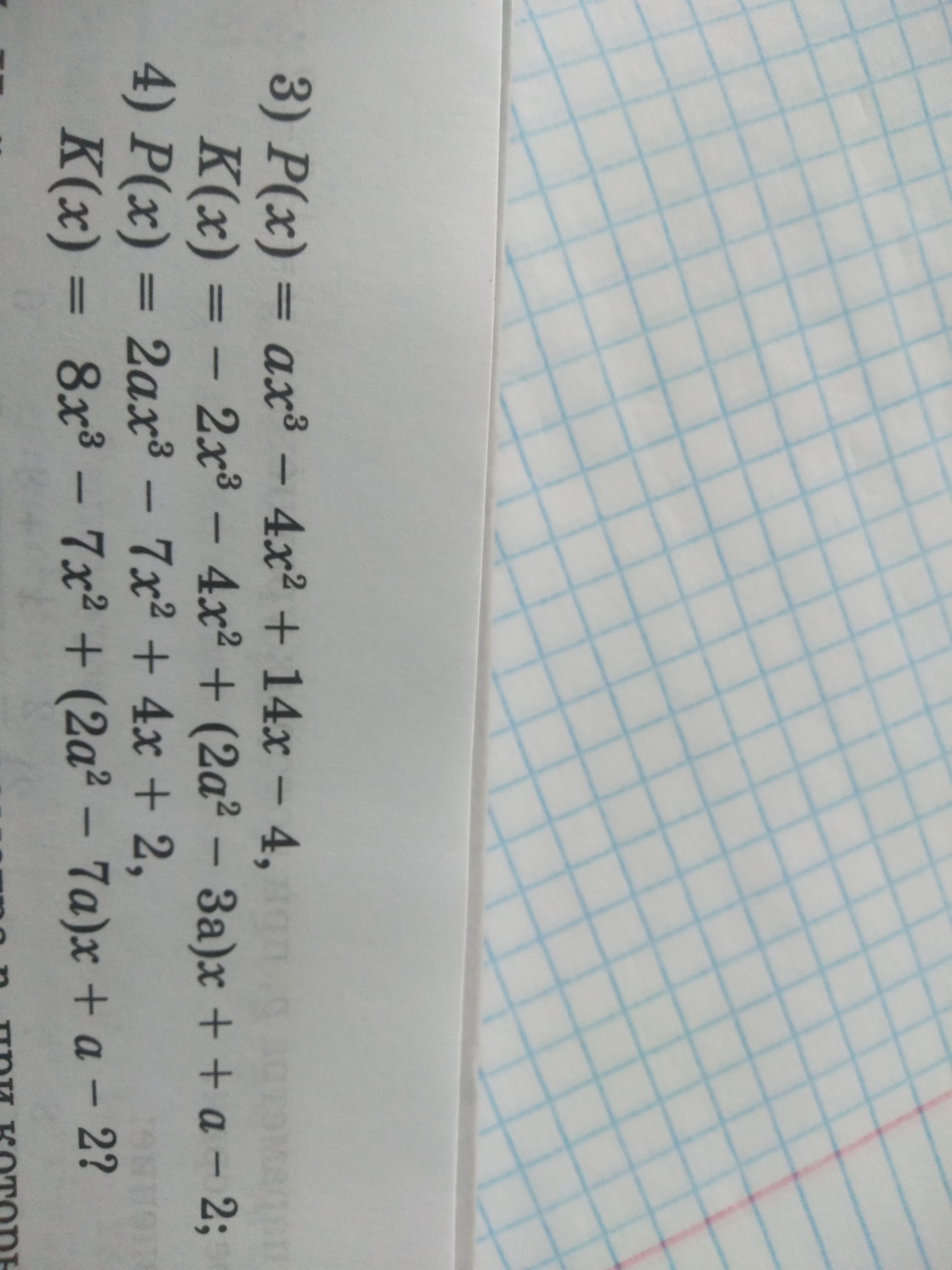
P(x)=x³–3x²+3x+2a²–3a–7
P(x)=x³+2x²–5x+a²–5a
P(x)=–x³+x²+2x+a²–a
При каких значениях a корень многочлена P (x) равен 2?

f (x) = (a ^ 2–7) x ^ 3–2x ^ 2 + (2a + 1) x–3 и g (x) = 2x ^ 3–2x ^ 2 + (a–2) xa–6 Каково значение a многочленов a:

Найдите рациональные корни уравнения

СРОЧНО!
1)Найдите значение параметра а, при котором многочлены f(x)=(a2–7)3–2x2+(2a+1)x–3 и g(x)=2x3+(a–2)x–a–6 тождественно равны

z⁶+3z³+2=z⁶+kz⁵+pz⁴+Mz³+z³+kz²+pz+M

(X⁵+2x³–x²–2) : (x³–1)

Разложить многочлен P(x) по степеням линейного (x–c) .P(x)=x3+ x2 –2 x; c=3.

целые корни многочлена 2x3+3x2–7x–10

Дан квадратный треугольник P₁ (x) = x ^ 2–x–6. Для этого треугольника выполняются уравнения P₂ (x) = P₁ (2x), P₃ (x) = P₂ (2x),…, P₁0 (x) = P₉ (2x). Решите уравнение P₁0 (x) = 0.

Известно, что f(x) — многочлен степени n и при всех значениях переменной х выполняется равенство f(x) = f(–x). Докажите:
1) n — четное натуральное число или нуль;
2) коэффициенты многочлена f(x) при нечетных степенях x равны 0.

При каких значениях a и с многочлен f(x) делится на многочлен h(x):
1) f(x) = x⁴ – 3x³ + 3x² + ax + c, h(x) = x² – 3x + 2;
2) f(x) = x⁴ – 2x³ + ax + 2, h(x) = x² + x + c?

найти наибольший член разложения бинома ( √5+2)¹³

Найдите разложение следующих полиномов:
1) (x + a)⁵;

Найдите разложение следующих полиномов:
(3х+2а)⁶

Найдите разложение следующих полиномов:
(3x – a)⁵;

Найдите остаток P(x)=2x⁴+7x³–2x²–13x+9 на (x+2)

Определите коэффициент x⁴ в классификации бинома (2–x) ⁵.

Разложите на множители: (a–b)9 и (3x+y)10

Представьте в виде многочлена степень:

(x+a)⁵
(3x+2a)⁶
(3x–a)⁵

Найдите коэффициент при хⁿ в разложении степени с помощью бинома Ньютона:

1) (x+2)¹⁰, n = 3 ...

Найдите значение суммы биномиальных коэффициентов разложения (a+b)¹¹

∑ (–1)^k C^k_n = 0

Найдите n в разложении степени бинома (3+1/√2)ⁿ‚ если отношение четвертого слагаемого разложения к третьему равно 3√2

3z5–z4–3z+1=(z2+1)(3z3+Kz2+Pz+M

ПОМОГИТЕ ПОЖАЛУЙСТА.
№1.Найти разложение степени бинома:
1)(x+y)⁴; 4)(b²+1)⁵
№2.Сумма всех биномиальных коэффициентов в разложении бинома (x+y)^n равна 512, найти n

Помогите пожалуйста
Найдите коэффициент при х^n в разложении степени с помощью бинома Ньютона:
1) (x+2)^ 10, n= 3;

Разложи на множители квадрaтный трёхчлен x² + 21x + 68.

Найти коэффициент при x⁴⁶ в разложении данного выражения (1–x⁴+x⁶)¹⁴ по полиномиальной формуле, полученной после раскрытия скобок и приведения подобных членов.

Найти коэффициент при x^k в разложении данного выражения P по полиномиальной формуле, полученный после раскрытия скобок и приведения подобных членов.

k– 57,
P– (2x–x³+x⁷)¹9

Выполните деление уголком многочлена

1) x³–2x²–3x–5 на многочлен x²–3x–1
...

Найдите значение суммы многочленов f(x) и h(x):
1)f(x)=2x³–3x²+5 и h(x)=3x²–x–6 при x=2;3;–1.
2)f(x)=5x⁴–3x²+1 и h(x)=x²–3x–1 при x=2;3;–1.
Найдите все значения параметров а и б ,при которых тождественно равны многочленыf(x)и h(x):
f(x)=2ax–(a+1)и h(x)=4x+(3b–a+11).

Выполнить задание деление уголком
Запишите многочлен 4–й степени корнями которого являются числа :
1)–2,0,2,3;
2)–3,–1,1,3

Помогите пожалуйста ,решить оба примера
Найдите остаток от деления на двучлен многочлена Р(х)
(Деление уголком )
P(x)=2x⁴+7x³–2x²–13x+4 на (x–1);
P(x)=x⁴+2x³+5x²+4x–12 на (х+2).

Создатель