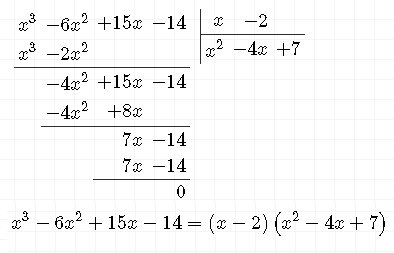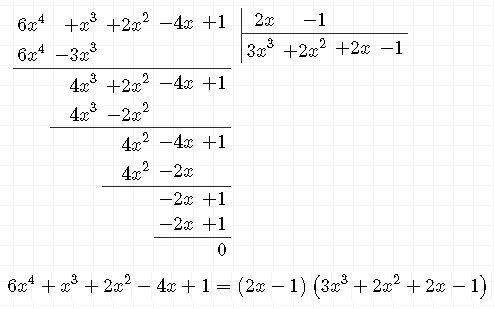Задача 57395 Найдите рациональные корни уравнения...
Условие
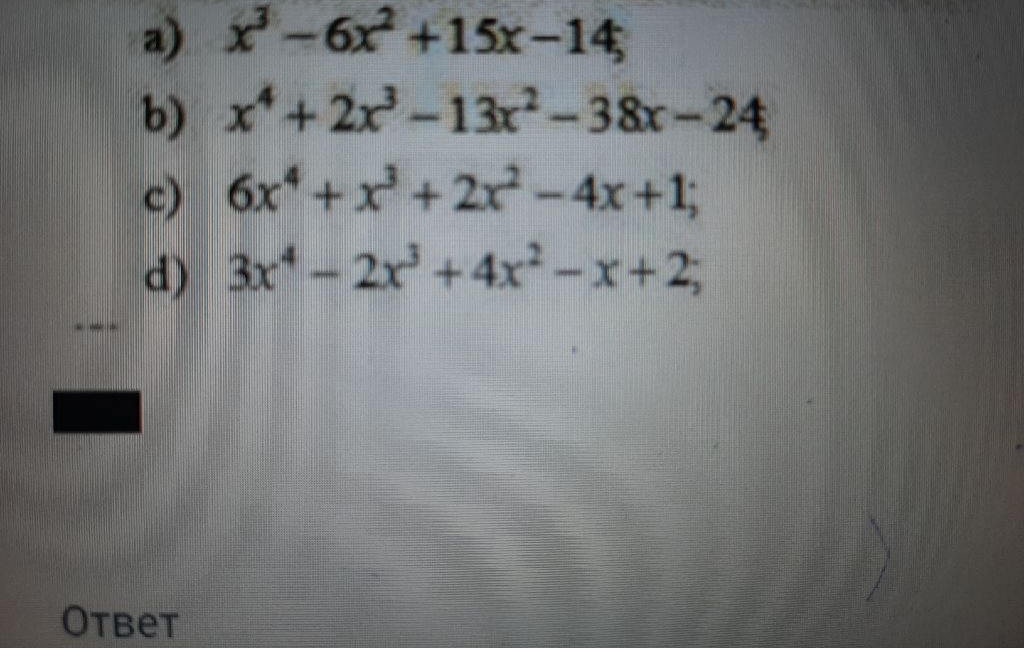
Решение
± 1; ± 2 ;± 7; ± 14
x=2 - корень многочлена, так как
2^3-6*2^2+15*2-14=0 - верно
38-38=0
x^3-6x^2+15x-14=(x-2)*(x^2-4x+7)
Квадратный трехчлен не имеет корней, D <0
О т в е т. x=2 - единственный корень
2)
Корни многочлена среди делителей свободного члена.
± 1; ± 2 ;± 3; ± 4; ± 6; ± 12; ± 24
x=-1 - корень многочлена, так как
(-1)^4+2*(-1)^3-13*(-1)^2-38*(-1)-24=0 - верно, 39-39=0
x^4+2x^3-13x^2-38x-24=(x+1)(x+2)(x+3)*(x-4)
3)
Корни многочлена среди дробей:
± 1; ± 1/2 ;±1/ 3; ±1/ 6
x=1/2 - корень
6x^4+x^3+2x^2-4x+1=(2x-1)*(3x^3+2x^2+2x-1)
x=1/3 - корень
3x^3+2x^2+2x-1=(3x-1)(x^2+x+1)
Квадратный трехчлен не имеет корней, D <0
О т в е т. 1/2; 1/3 - корни многочлена
4)
Корни многочлена среди дробей:
± 1; ± 1/3 ;±2/ 3
Нет корней
3x^4-2x^3+4x^2-x+2=(3x^2+px+q)(x^2+mx+n)
и каждый квадратный трехчлен не имеет корней, так как дискриминанты отрицательные