Задача 62056 сколько членов разложения бинома...
Условие
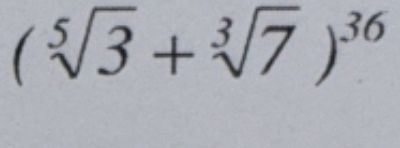
Решение
[m](a+b)^{n}=C^{0}_{n}a^{n}b^{0}+C^{1}_{n}a^{n-1}b^{1}+C^{2}_{n}a^{n-2}b^{2}+...+C^{k}_{n}a^{n-k}b^{k} +...+C^{n}_{n}a^{0}b^{n}[/m]
[m]T_{k}=C^{k}_{n}a^{n-k}b^{k} [/m]
n=36
[m]a=\sqrt[5]{3}[/m]
[m]b=\sqrt[3]{7}[/m]
[m]T_{k}=C^{k}_{36}(\sqrt[5]{3})^{36-k}(\sqrt[3]{7})^{k}[/m]
[m]C^{k}_{36}[/m] - целые ( см. треугольник Паскаля)
Значит, чтобы слагаемое разложения было целым, достаточно, чтобы
[m](\sqrt[5]{3})^{36-k}(\sqrt[3]{7})^{k}=3^{\frac{36-k}{5}}\cdot 7^{\frac{k}{7}}[/m] было целым.
А это означает, что
36-k должно быть кратно 5
и
k должно быть кратно 7
36-k кратно 5 при k=1; [b]6[/b];11;16;[b]21[/b];26;31;[b]36[/b]
k кратно 3 при k=0;3;[b]6[/b];9;12;15;18;[b]21[/b];24;27:30;33;[b]36[/b];
При k=6
[m](\sqrt[5]{3})^{36-6}(\sqrt[3]{7})^{6}=3^{6}\cdot 7^{2}[/m]- целое.
При k=21
[m](\sqrt[5]{3})^{36-21}(\sqrt[3]{7})^{21}=3^{3}\cdot 7^{3}[/m]- целое.
При k=36
[m](\sqrt[5]{3})^{36-36}(\sqrt[3]{7})^{36}=3^{0}\cdot 7^{12}[/m]- целое.
О т в е т. три члена разложения целые