Задача 57655 ...
Условие

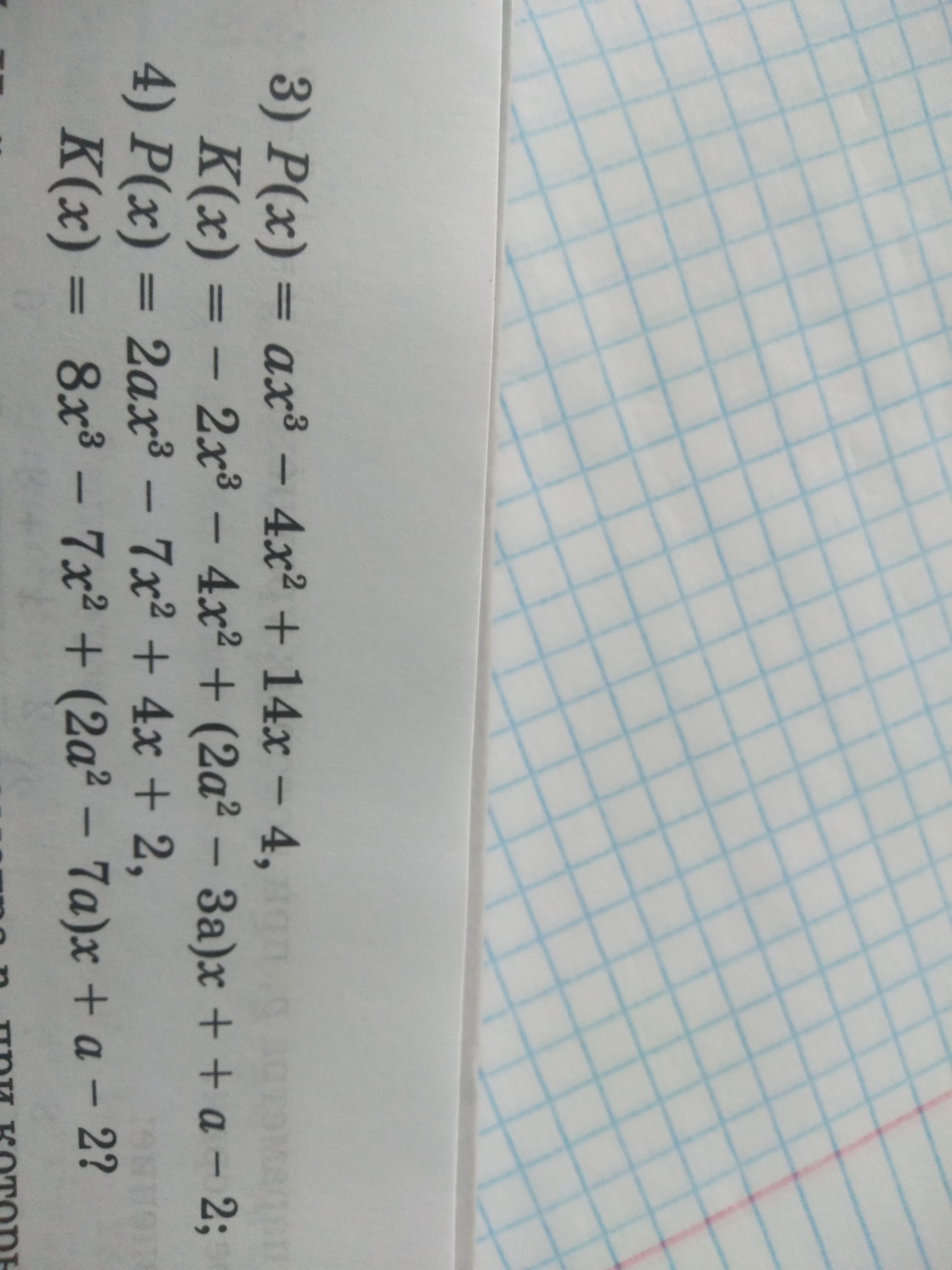
Решение
1) равны их степени;
2) равны коэффициенты при одинаковых степенях
[red] 1задание [/red]
1) оба многочлена имеют третью степень
2)
при x^3
(2-a ^ 2)=а
при x^2
3=a^2+2a
при х^1
2 = 2
при x^(0), т. е свободные
-9= -9
Все эти равенства должны выполняться одновременно, т.е находим а из системы:
{2-a ^ 2=a ⇒ a^2+a-2=0 ⇒ D=9; a_(1)= -2; [b]a_(2)=1[/b]
{3=a^2+2a ⇒ a^2+2a-3=0 ⇒ D=16; a_(3)= -3; [b]a_(4)=1[/b]
[b]a_(2)=a_(4)=1[/b]- общее решение системы
О т в е т. При[b] a=1[/b]
[red]2 задание [/red]
{2a=-2 ⇒ [b]a=-1 [/b]
{-14=14a ⇒ [b]a= -1[/b]
{3=2a^2-a ⇒ 2a^2-a-3=0 ⇒ D=25; a= 3/2; [b] a=-1[/b]
{4=a+5 ⇒ [b]a=-1[/b]
[b]a=-1[/b]- общее решение системы
О т в е т. При [b]a=-1[/b]
[red]3 задание [/red]
{[b]a=-2 [/b]
{14=2a^2-3a ⇒ 2a^2-3a-14=0 ⇒ D=121; a= 7/2; [b]a=-2[/b]
{-4=a-2 ⇒[b] a=-2[/b]
[b]a=-2[/b]- общее решение системы
О т в е т. При [b]a=-2[/b]
[red]4 задание [/red]
{2a=8 ⇒ [b]a=4 [/b]
{4=2a^2-7a ⇒ 2a^2-7a-4=0 ⇒ D=81; a= -1/2; [b]a=4[/b]
{2=a-2 ⇒[b] a=4[/b]
[b]a=4[/b]- общее решение системы
О т в е т. При [b]a=4[/b]