Функции: область определения, область изменения, период, четность, нечетность
Практика (49)
у = -2х – 6 и у = 3х – 6 и запишите координаты точки пересечения этих графиков.
1) y=4x-2
2)y=x+3
3) y=4x+2
4) y=x-3

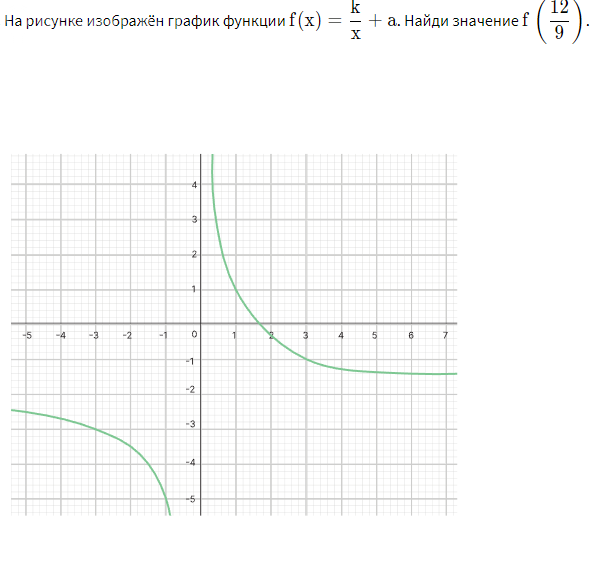
13.9сравнить значения выражения

f(x)=3-0,5x
1) определить координаты вершины параболы
2) найти точку пересечения с осью Оу
3) найти точку пересечения с осью Ох
4) построить график функции 
Определите действительные значения параметра m, для которых графики функции является парабола с ветвями направленными вниз и имеет одну общую точку с осью абсцисс


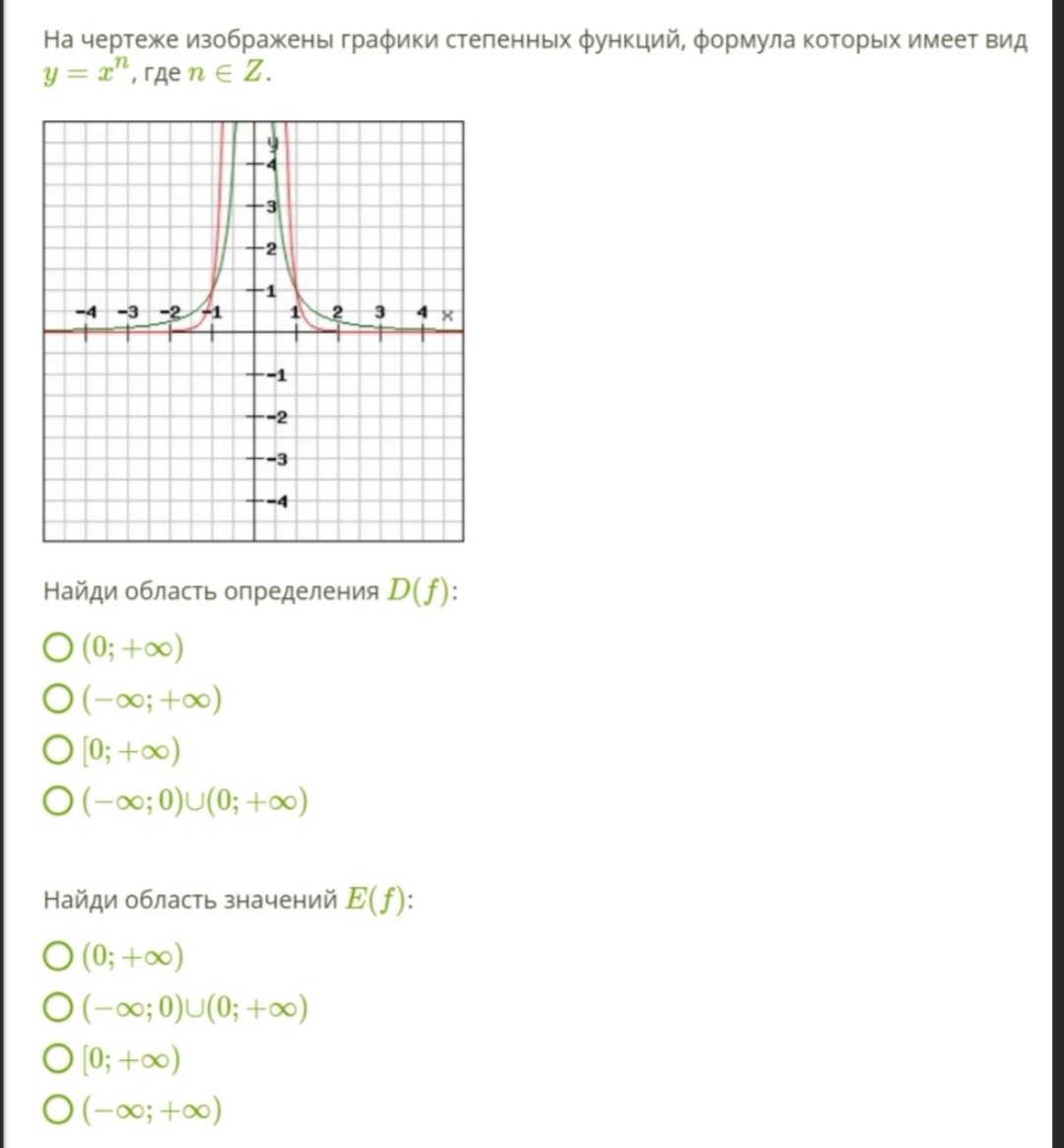
А) область определения функции;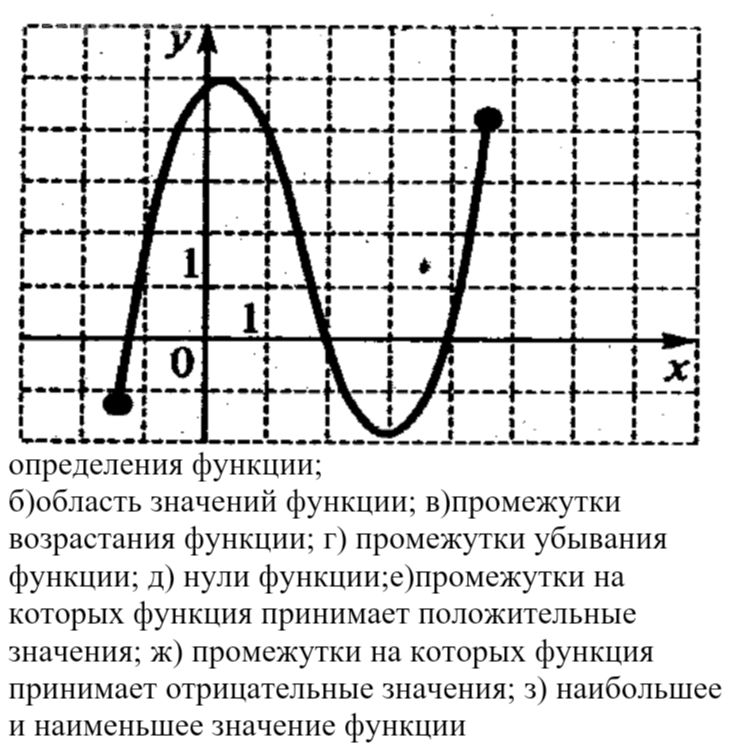
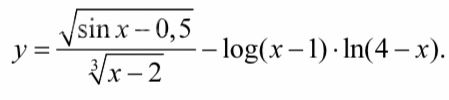
2. Найти нули функции, если ...
3. Найти ...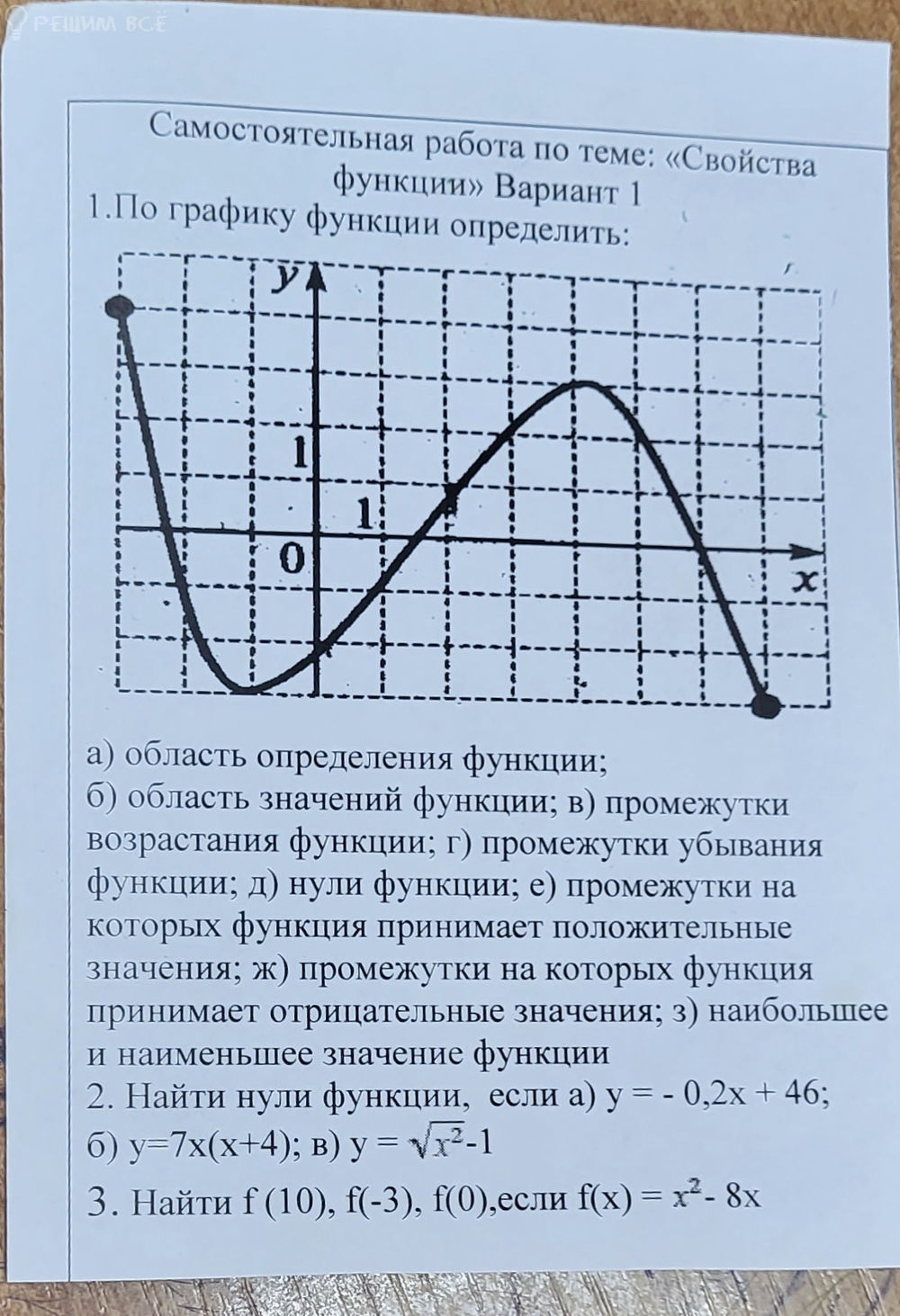
1) f(x)=x+1 у точках 2; -1; 3; а (a≠0);
2) g(x)=x^2-3 у точках 0; 1; -2; b;
3) φ(x)=√x+1 у точках 0; 3; -1; m (m>0).
1.2.2. Знайдіть область визначення функції, заданої формулою:
1°) y=2x+3; 3°) y=1/(x+1); 5°) y=√(x^2-1); 7°) y=√(x-1)+√(5-x);
2°) y=√(x+3); 4°) y=x/(x+1); 6°) y=√(x^2+1); 8°) y=√(x+3).
проходя через точку В(3;-1)Покажите что точка А(6;-0,5) принадлежит графику функции f.
1. А(-5; 8).
2. В(1/3; -6)
y = √((3-x) / (x^2 - x - 2)),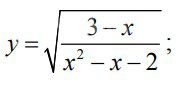
Определите координаты точки пересечения графика функции f с осью абсцисс. 
1) f(x) = 1/x ; g(x) = x^2 + 1;
2) f(x) = 0 при х ≤ 0; x при х > 0; g(x) = x^2 - 1.
у=-х²+4х-3
Используя график, найдите:
а) значение аргумента если значение функции равно:-3;1;0
b) значение функции если значение аргумента равно 4;0;3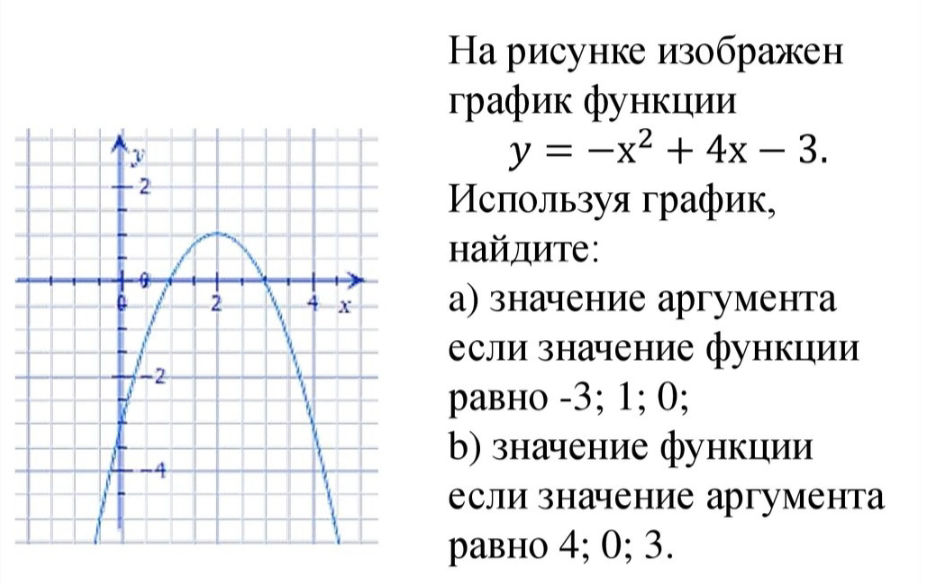
3) y = 1/(x-2) + √((x-2)/(x^2-9));
4) y = 1/(x^2-4) + √(x^2-16)/(x+3).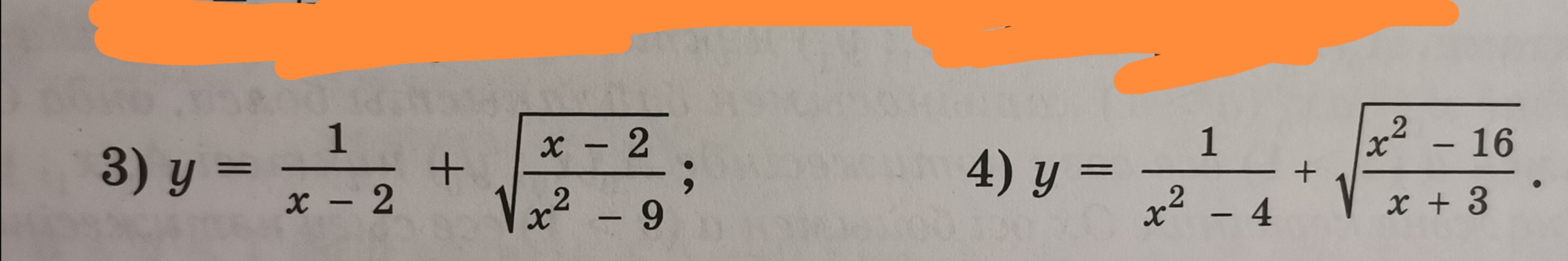

вертикально вверх камня вычисляют по
формуле h(t) = –3t² + 18t, где h — высота в
метрах,
t — время в секундах, прошедшее с момента
броска.
а) Через сколько секунд мяч будет находиться
на высоте 15м?
б) На какой высоте будет мяч через 4 с?
в) На какую наибольшую высоту подымется
камень и в какое время.

y = (sqrt(4x - x^2)) / (log3|x - 4|)
b) y=1/x^2+1
1) параллельна оси Ox;
2) не существует;
3) составляет с положительным направлением оси Ox угол в 45°.
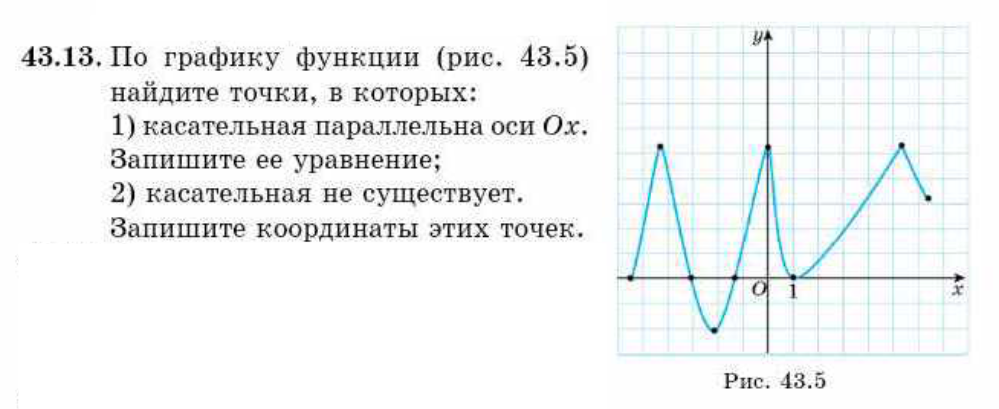
43.13. По графику функции (рис. 43.5) найдите точки, в которых:
1) касательная параллельна оси Ox. Запишите ее уравнение;
2) касательная не существует. Запишите координаты этих точек.
y=sqrt(6x-1)+sqrt(8-4x)
{x^2 + 8x + 11,x ≤ -2
{-x - 2,x ∈ (-2; 0].
Решите уравнение f(x) = x/2
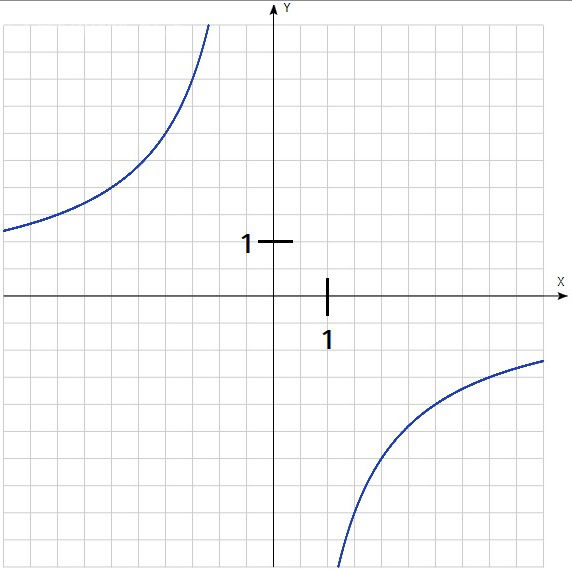
[m]\displaystyle{y = \frac{1}{x + b} + a}[/m]
Введи [m]a =[/m] [m]\_[/m].
Введи [m]b =[/m] [m]\_[/m].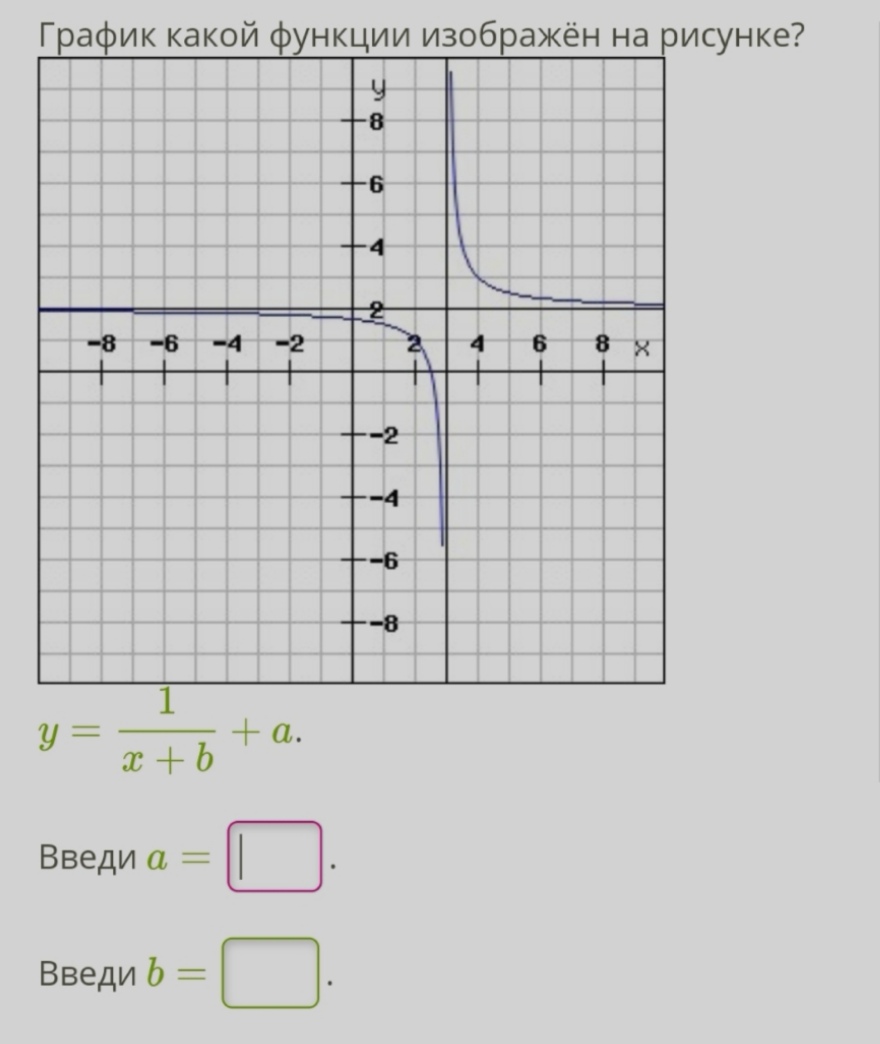
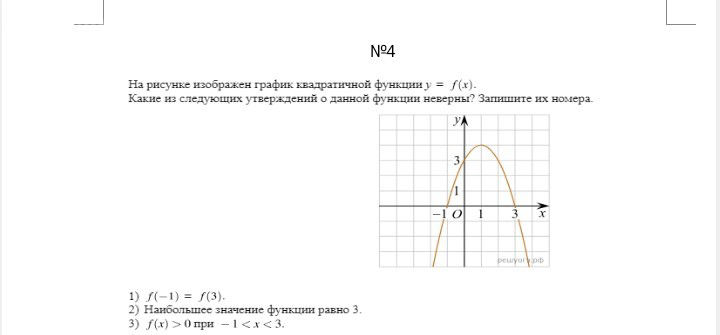
б) значения функции составляют промежуток [–4; 4];
в) в левом конце области определения функция принимает наибольшее значение;
г) значения функции отрицательны только в точках промежутка (–2;1);
д) –1 – единственная точка экстремума функции.
Редакторы (1)
 SOVA
SOVA
Создатель