Задача 55051 найдите область определения функции...
Условие
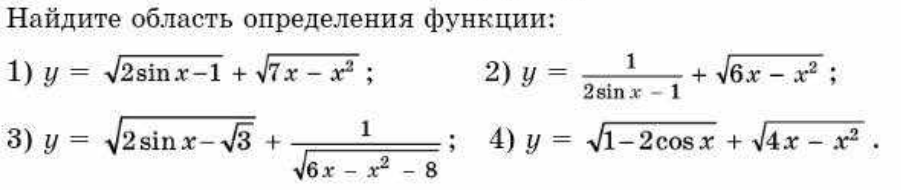
Решение
2sinx-1 ≥0 \\7x-x^2 ≥ 0 \end{matrix}\right.[/m] ; [m]\left\{\begin{matrix}
sinx ≥ \frac{1}{2} \\x^2-7x ≤ 0 \end{matrix}\right.[/m]
Решаем первое неравенство:
[m]\frac{π}{6}+2π n ≤ x ≤ \frac{5π}{6}+2π n , n \in Z[/m]
Решаем второе методом интервалов:
__________+____ [0] __-__ [7]____+____
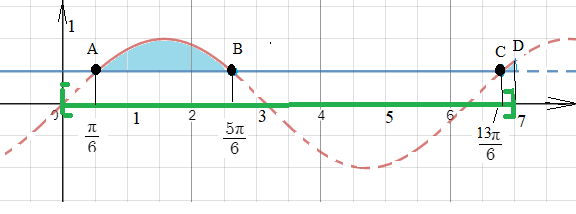
Пересечение множеств решений первого и второго неравенств - рассматриваем часть графика y=sinx на [0;7]
Системе удовлетворяют точки дуги AB и дуги СD синусоиды.
Поэтому
[m]x \ in [\frac{π}{6};\frac{5π}{6}]\cup[\frac{13π}{6};7][/m]
О т в е т. [m][\frac{π}{6};\frac{5π}{6}]\cup[\frac{13π}{6};7].[/m]
Аналогично
2)
[m]\left\{\begin{matrix}
2sinx-1 >0 \\6x-x^2 ≥ 0 \end{matrix}\right.[/m] ; [m]\left\{\begin{matrix}
sinx >\frac{1}{2} \\x^2-6x ≤ 0 \end{matrix}\right.[/m]
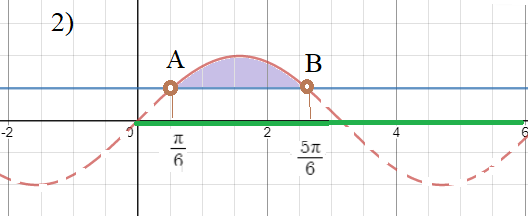
Рассматриваем часть графика y=sinx на [0;6]
Системе удовлетворяют точки дуги AB синусоиды.
причем точки А и В не входят, неравенство строгое
Поэтому
[m]x \ in (\frac{π}{6};\frac{5π}{6})[/m]
О т в е т. [m](\frac{π}{6};\frac{5π}{6})[/m]
3)
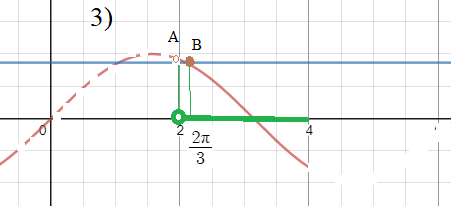
Рассматриваем часть графика y=sinx на (2;4) ( второе неравенство строгое)
Системе удовлетворяют точки дуги AB синусоиды.
точка А не входит, неравенство строгое
О т в е т. (2; 2π/3]